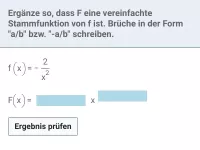
Was sind die Stammfunktionen von exp(x), sin(x) und cos(x) und was ist bei der Integration von f(ax+b) zu beachten?

  • Stammfunktionen von sin, cos und exp:

∫ sin (x) dx = − cos (x) + C

∫ cos (x) dx = sin (x) + C

∫ ex dx = ex + C

  • Beachte aufgrund der Kettenregel (a ≠ 0):

∫ f ( ax + b ) dx

= 1/a · F ( ax + b) + C

Beispiel
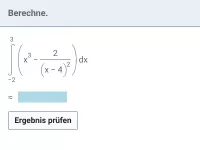
Gib jeweils eine Stammfunktion an.
a) 
f
 
x
=
2e
4x
+
1
a) 
f
 
x
=
sin
 
0,5x
−
π
Lösung zu a)
f
 
x
=
2e
4
x
+
1
F
 
x
=
2
4
 
e
4x
+
1
=
0,5e
4x
+
1
Erläuterung: da im Argument der e-Funktion der lineare Term 
4x
+
1
 steht, dessen Ableitung "4" ist, muss durch 4 geteilt werden. Man kann sich von der Korrekteit überzeugen, indem man die Stammfunktion probeweise wieder ableitet. Beachte dabei die Kettenregel:
F ´
 
x
=
0,5e
4
x
+
1
·
4
=
2e
4x
+
1
=
f
 
x

Lösung zu b)
f
 
x
=
sin
 
0,5
x
−
π
F
 
x
=
1
0,5
·
−
cos
 
0,5x
−
π
=
−
2cos
 
0,5x
−
π
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen