Wie berechnet man die Stammfunktion einer Potenzfunktion?
Stammfunktion einer Potenzfunktion: Für alle ganzen Zahlen n ≠ -1 gilt
∫ xn dx = 1 / (n + 1) · xn + 1 + C
Man geht also umgekehrt zum Ableiten vor: beim Ableiten wird zuerst mit n multipliziert, dann der Exponent n um 1 reduziert. Beim Bilden der Stammfunktion wird zuerst der Exponent n um 1 vergrößert, dann durch n+1 geteilt.
Spezialfall n = -1:
∫ 1/x dx = ln |x| + C
Beispiel 1
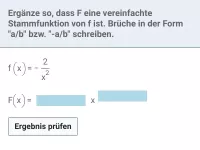
Gib eine Stammfunktion für
an.
| = |
|
| = |
| |||||||||||||||||||||||||||
|
| = |
| kürzen | ||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||

Lernvideo
Uneigentliche INTEGRALE berechnen – e Funktion gegen unendlich, Definitionslücke, 1. und 2. Art
Kanal: MathemaTrick
Beispiel 2
Gib eine Stammfunktion für
an.
| = |
|
| = |
| ||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||
|
| = |
| kürzen | |||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||||
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff + Video
Integral - Berechnung mit Stammfunktion
Stammfunktion von Potenz-, trigonometrischer und natürlicher Exponentialfunktion (auch zusammengesetzt), bestimmtes Integral mit Hilfe von Stammfunktion berechnen -
≈Oberstufe - Aufgaben + Stoff + Video
Stammfunktion
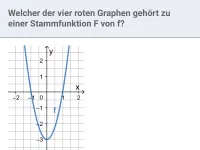
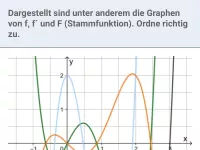
Zeigen, dass F(x) Stammfunktion von f(x) ist; F(x) nach Ableitungsregel (rückwärts) ermitteln; Graphen von F und f einander zuordnen; Eigenschaften von F und f graphisch ermitteln
Ähnliche Themen
- Was ist eine Stammfunktion F von f und welche Beziehung besteht zwischen den Werten von f und F?
- Was versteht man unter der "Ableitungskette" in Bezug auf Funktionen und ihre Graphen?
- Wie findet man die Stammfunktion eines Bruchterms, wenn im Zähler die Ableitung des Nenners steht?
- Was sind die Stammfunktionen von exp(x), sin(x) und cos(x) und was ist bei der Integration von f(ax+b) zu beachten?