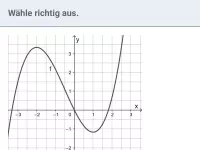
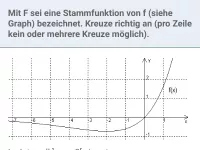
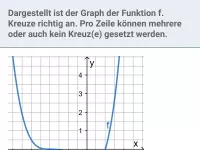
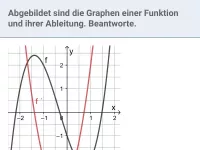
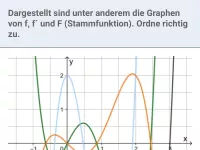
Was ist eine Stammfunktion F von f und welche Beziehung besteht zwischen den Werten von f und F?
Die Funktion F ist genau dann eine Stammfunktion von f, wenn F´ = f (wenn also f die Ableitung von F ist). Damit gilt folgender Zusammenhang
| F bzw. GF | f (x) |
| streng monoton steigend | > 0 im betrachteten Intervall |
| streng monoton fallend | < im betrachteten Intervall |
| keine Steigung (waagrechte Tangente) | = 0 |
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff + Video
Differenzierbarkeit und Ableitungsfunktion
Untersuchung von abschnittsweise definierten Funktionen und Betragsfunktion auf Differenzierbarkeit; Zusammenhang zwischen f, f´ und F (Stammfunktion) anhand von Graphen -
≈Oberstufe - Aufgaben + Stoff + Video
Stammfunktion
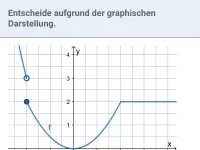
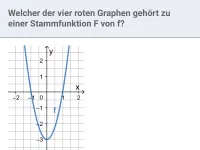
Zeigen, dass F(x) Stammfunktion von f(x) ist; F(x) nach Ableitungsregel (rückwärts) ermitteln; Graphen von F und f einander zuordnen; Eigenschaften von F und f graphisch ermitteln
Ähnliche Themen
- Was zeigt das Vorzeichen der Ableitung f'(x) einer Funktion an?
- Was versteht man unter der "Ableitungskette" in Bezug auf Funktionen und ihre Graphen?
- Wie berechnet man die Stammfunktion einer Potenzfunktion?
- Wie erkennt man graphisch, dass eine Funktion an einer Stelle nicht differenzierbar ist?
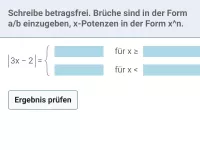
- Wie kann man einen von Betragsstrichen umgebenen Term betragsfrei schreiben?