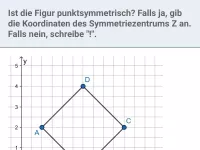
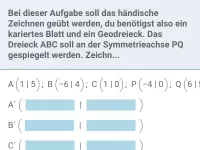
Wann liegen zwei Punkte symmetrisch zu einer Achse?
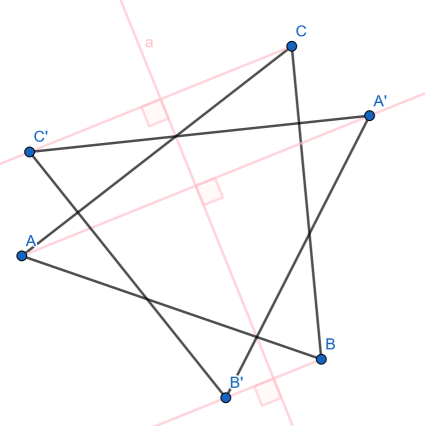
Zwei Punkte P und P´ liegen symmetrisch bzgl der Achse a, wenn ihre Verbindungsstrecke senkrecht auf der zur Achse a steht und von dieser halbiert wird.
Beispiel
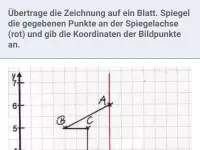
Das Dreieck ABC soll an der Achse a gespiegelt werden:
Lösung: Zeichne von A, B und C aus jeweils eine Halbgerade, die senkrecht zur Achse a steht.
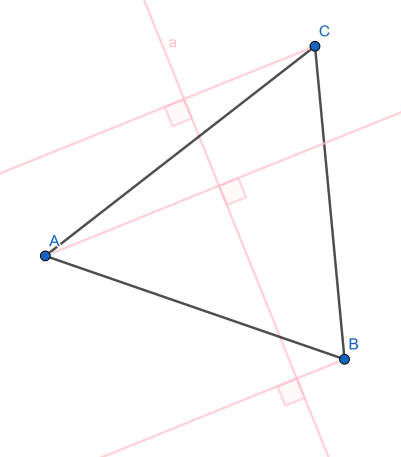
Trage dann auf jeder Halbgeraden, gegenüber und gleichweit entfert, den jeweiligen Bildpunkt ein (Konstruktion: Zirkel im Schnittpunkt von Achse und jeweiliger Halbgerade einstechen und dann Kreis um den Eckpunkt zeichnen).
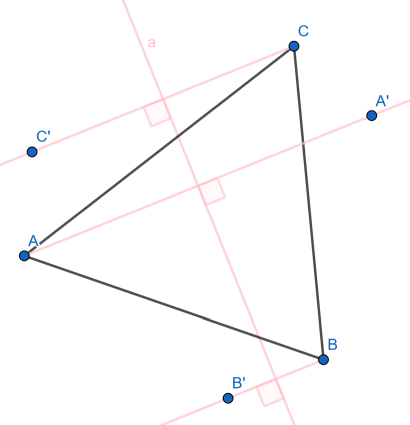
Jetzt müssen A´, B´ und C´ nur noch verbunden werden.