Was ist bei der Formulierung von Null- und Gegenhypothese sowie kritischem und unkritischem Bereich zu beachten?

Checkliste bei der Festlegung von Null- und Gegenhypothese sowie kritischem und unkritischem Bereich:
  • H0 lautet "p =", "p ≤" oder "p ≥" ("=" kommt vor).
  • H1 lautet dagegen "p >" oder "p <" ("=" kommt nicht vor).
  • H1 und K (Ablehnungsbereich der Nullhypothese) verwenden dasselbe Ungleichheitszeichen
  • K und K decken zusammen den kompletten Stichprobenumfang ab und dürfen sich nicht überschneiden.
Beispiel
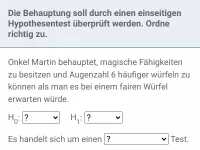
Ein Würfel ist angeblich gezinkt und bringt Augenzahl 6 deutlich häufiger hervor als alle anderen Augenzahlen. Dies soll durch 60 Würfe getestet werden. Fällt dabei "Augenzahl 6" mehr als 15 mal, so gilt der Verdacht als bestätigt. Formuliere H0 und H1 sowie kritischen und unkritischen Bereich.
Lösung:
  • Null- und Gegenhypothese
Bei einem normalen Würfel ist die Wahrscheinlichkeit für "Augenzahl 6" genau 1/6. Stimmt der Vorwurf, so ist diese Wahrscheinlichkeit größer als 1/6. Man formuliert also:
H
0
:
 
p
 
=
 
1
6
 
 
normaler Würfel
H
1
:
 
p
 
>
 
1
6
 
 
gezinkter Würfel
Beachte, dass zu H0 immer das "=" gehört. Eine umgekehrte Zuordnung (H0 und H1 vertauscht) wäre also falsch.
  • K und K
Hier stehen sich die Intervalle 
Z > 15
 ("mehr als 15 mal", also 16; 17; ...60) und 
Z ≤ 15
 (also 0; 1; ...15) gegenüber. Es ist klar, dass 
Z > 15
 zur Gegenhypothese gehört und damit den kritischen Bereich definiert, da bei der Gegehypothese ebenso ">" (nach recht geöffnet) steht.
H
0
:
 
p
 
=
 
1
6
 
 
 
 
 
K
:
 
Z
 
≤
 
15
H
1
:
 
p
 
>
 
1
6
 
 
 
 
 
 
 
K
:
 
Z
 
>
 
15
Beachte, dass 
K
: Z < 15
 falsch wäre, da dann 
Z
=
15
 weder durch K noch durch K abgedeckt wäre.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen