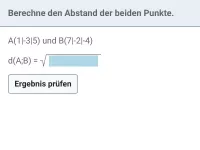
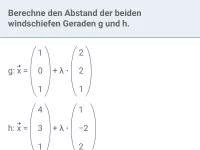
Lösung:
Bemerkung: farbig markiert sind die Koordinaten von P, die für die x-Koordinaten eingesetzt wurden.
- - - - - - - - - - - - - - - - - -
Falls dich interessiert, WARUM man so rechnet, kannst du dir die Zeichnung anschauen und anhand dieser die Erklärungsschritte nachverfolgen:
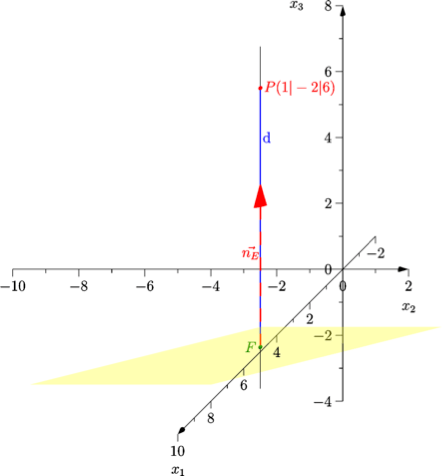
Der Abstand (bzw. die kürzeste Entfernung) von P zur Ebene E entspricht der Länge d des Lotes von P auf die Ebene E. Um diese Länge zu ermitteln wird der Lotfußpunkt F benötigt.
Geradengleichung des Lotes durch P bestimmen:
Als Fußpunkt der Geradengleichung wird der Punkt P verwendet. Der Richtungsvektor der Geradengleichung ist der Normalenvektor der Ebene E, der aus der gegebenen Normalenform von E direkt abgelesen werden kann.
Koordinaten des Lotfußpunkts F bestimmen (Schnittpunkt des Lotes mit der Ebene E):
Dazu wird die Geradengleichung des Lotes koordinatenweise in die Ebenengleichung eingesetzt.
|
| = |
| vereinfachen |
|
|
| = |
| zusammenfassen |
|
|
| = |
| |
|
|
| = |
| |
|
|
| = |
| |
|
Bemerkung: farbig markiert sind die Koordinaten der Lotgerade, die für die x-Koordinaten der Ebenengleichung eingesetzt wurden.
Um die Koordinaten des Lotfußpunktes F zu erhalten, wird μ jetzt in die Lotgerade eingesetzt:
Abstand von P zur Ebene E berechnen (entspricht Berechnung der Länge von [PF]):