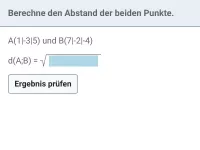
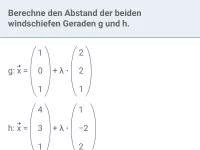
Wie bestimmt man den Abstand eines Punktes zu einer Geraden? Erläutere zwei Methoden.
Hier zwei alternative Vorgehensweisen, um den Abstand eines Punktes P von einer Geraden g zu bestimmen:
Mittels Hilfsebene:
- Führe eine Hilfsebene E ein, die P enthält und senkrecht zu g verläuft (also den Richtungsvektor von g als Normalenvektor besitzt).
- Ermittle den Schnittpunkt S von E und g.
- Berechne die Entfernung zwischen P und S.
Oder mit Hilfe des "Verbindungsvektors":
- Bilde den Vektor, der P mit einem Punkt Qλ der Geraden g verbindet.
- Bestimme λ so, dass der Verbindungsvektor senkrecht zu g steht (also das Skalarprodukt mit dem Richtungsvektor von g den Wert 0 ergibt).
- Berechne jetzt die Länge des senkrechten Verbindungsvektors.
Beispiel
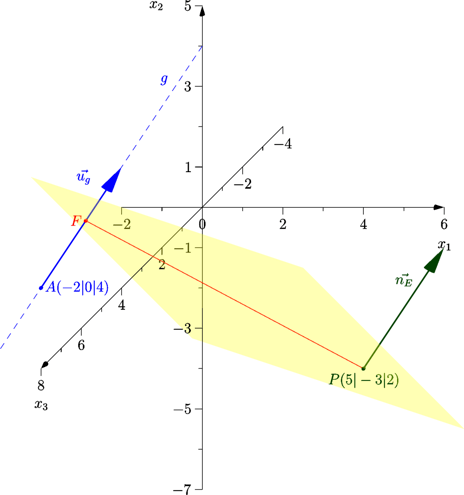
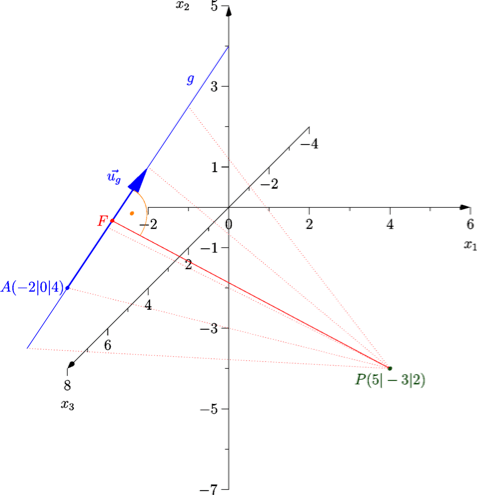
Welchen Abstand hat der Punkt P(5|-3|2) von der Geraden g:
?
X
| = |
|
Der Abstand zwischen P und g ist als Länge der senkrechten Verbindungsstrecke von P zur Geraden g zu verstehen.
Lösungsmöglichkeit 1: mittels Hilfsebene
Idee:
1. Führe eine Hilfsebene E ein, die P enthält und senkrecht zu g verläuft. Jede Gerade in der Ebene liegt dann senkrecht zu g.
2. Bestimme den Schnittpunkt (Lotfußpunkt F) von g und E.
3. Berechne die Länge des Verbindungsvektors
.
PF
1. Schritt: Ebenengleichung aufstellen
Da g senkrecht zur Ebene stehen soll, wählen wir den Richtungsvektor der Geraden als Normalenvektor der Ebene.
Da P in der Ebene liegen soll, wählen wir den Ortsvektor von P als Aufpunkt der Ebene.
Damit lautet die Normalen- bzw. Koordinatengleichung der Ebene:
| = | 0 |
| = | 0 |
| = | 0 |
| = | 0 |
2. Schritt: Lotfußpunkt berechnen
Für den Schnittpunkt der Geraden g mit der Ebene E wird g "koordinatenweise" in E eingesetzt, dies ist blau markiert. Die entstehende Gleichung kann nach λ aufgelöst werden.
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| :9 | |||||||||||||||||||||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
λ in g einsetzen liefert den Lotfußpunkt F:
| = |
|
bzw. F(
|
|
)
|
|
1 |
|
2 |
|
3. Schritt: Länge des Verbindungsvektors
berechnen.
PF
| = |
|
| = |
|
Der Abstand von P zur Geraden g beträgt damit
.
| ≈ 7,7 |
---------------
Lösungsmöglichkeit 2: mittels Verbindungsvektor
Idee:
1. Ermittle den Verbindungsvektor von P zu einem beliebigen Punkt
auf der Geraden (der vom Parameter λ abhängt!).
F | λ |
2. Suche denjenigen Punkt F, für den der Verbindungsvektor senkrecht zur Geraden ist: Das Skalarprodukt von
und
ist in diesem Fall gleich Null.
PF | λ |
u
| g |
3. Berechne die Länge des senkrechten Verbindungsvektors.
1. Schritt: Verbindungsvektor
bestimmen.
PF | λ |
F | λ |
| = |
|
2. Schritt: Skalarprodukt gleich Null setzen
| = | 0 |
| = | 0 |
| = |
| zusammenfassen | |||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
| :9 | |||||||||||||||||||
| = |
| ||||||||||||||||||||
Jetzt geht es weiter wie im Lösungsvorschlag 1: λ in g einsetzen liefert denjenigen Geradenpunkt F, dessen Verbindungsvektor mit P senkrecht zu g steht. Dessen Länge liefert den gesuchten Abstand von P zu g.

Lernvideo
Koordinatengeometrie im Raum, Abstand Punkt Gerade, Beispiel
Kanal: Mathegym
Siehe auch