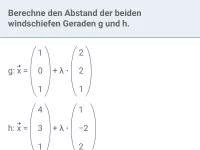
Wie kann man den Abstand zwischen zwei windschiefen Geraden g und h berechnen?
Hier zwei alternative Vorgehensweisen, um den Abstand zweier windschiefer Geraden g und h zu bestimmen:
Mittels Hilfsebene:
- Führe eine Hilfsebene E ein, die g enthält und parallel ist zu h (für die Gleichung von E in Parameterform kann man den Aufpunkt von g und die Richtungsvektoren beider Geraden verwenden).
- Wandle E in Normalenform um.
- Bestimme den Abstand zwischen dem Aufpunkt von h und der Hilfsebene E.
- Bilde den Vektor, der einen Punkt Pλ der Geraden g mit einem Punkt Qμ der Geraden h verbindet.
- Bestimme λ und μ so, dass der Verbindungsvektor senkrecht zu g und h steht (also das Skalarprodukt mit den Richtungsvektoren von g und h jeweils den Wert 0 ergibt).
- Berechne jetzt die Länge des senkrechten Verbindungsvektors.
Beispiel
Bestimme den Abstand der beiden Geraden g und h:
g:
x
| = |
|
h:
x
| = |
|
Der Abstand zwischen zwei windschiefen Geraden g und h ist die Länge der Verbindungsstrecke, die auf beiden Geraden g und h senkrecht steht.
Lösungsmöglichkeit 1: mittels Hilfsebene
Idee:
1. Führe eine Hilfsebene E ein, die g enthält und parallel ist zu h.
2. Wandle E in Normalenform/Koordinatenform um.
3. Bestimme den Abstand zwischen dem Aufpunkt von h und der Hilfsebene E.
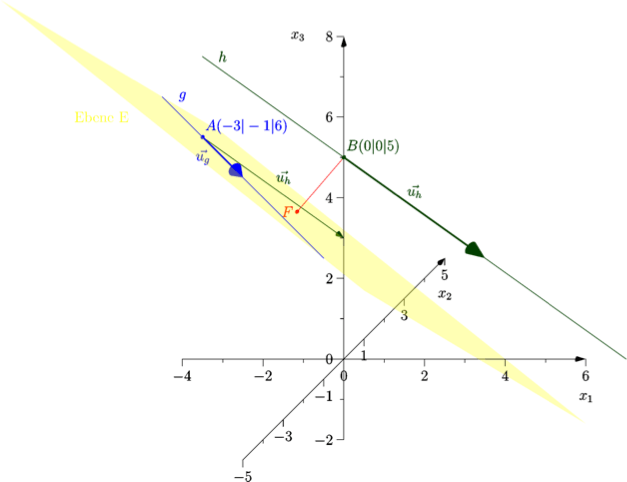
1. Schritt: Ebenengleichung aufstellen
Da g in der Ebene liegen soll, wählen wir den Aufpunkt von g auch als Aufpunkt der Ebene. Außerdem kann der Richtungsvektor der Geraden g als erster Richtungsvektor der Ebene gewählt werden.
Da die Gerade h parallel zur Ebene liegen soll, wählen wir den Richtungsvektor von h als zweiten Richtungsvektor der Ebene.
Damit lautet die Parametergleichung der Ebene:
E:
x
| = |
|
2. Schritt: Normalengleichung der Ebene
Das Vektorprodukt der beiden Richtungsvektoren liefert einen Normalenvektor der Ebene:
| = |
|
| = |
|
Damit lautet die Normalen- bzw. Koordinatengleichung der Ebene:
| = | 0 |
| = | 0 |
| = | 0 |
| = | 0 |
3. Schritt: Abstand vom Aufpunkt der Geraden h zur Ebene
Da die Gerade h parallel zur Ebene liegt, kann ein beliebiger Punkt von h (zum Beispiel der Aufpunkt B) gewählt werden, um den Abstand von h zur Ebene zu bestimmen. Im Bild oben ist dieser Abstand durch die rote Strecke vom Aufpunkt B zum Lotfußpunkt F dargestellt.
Berechnung des Abstands von B zur Ebene E:
| = |
|
Bemerkung: blau markiert sind die Koordinaten von B, die für die x-Koordinaten eingesetzt wurden.
Der Abstand zwischen den beiden windschiefen Geraden g und h beträgt damit
LE.
| 1,46 |
---------------
Lösungsmöglichkeit 2: mittels Verbindungsvektor
Idee:
1. Bilde den Vektor, der einen beliebigen Punkt
der Geraden g mit einem Punkt
der Geraden h verbindet.
P | λ |
Q | μ |
2. Bestimme λ und μ so, dass der Verbindungsvektor senkrecht zu g und senkrecht zu h steht.
3. Berechne die Länge des senkrechten Verbindungsvektors.
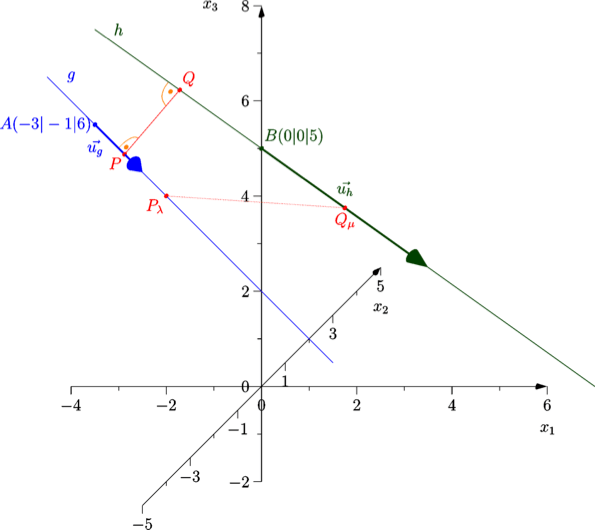
1. Schritt: Verbindungsvektor
bestimmen.
|
|
P | λ |
Q | μ |
Verbindungsvektor:
| = |
|
2. Schritt: Bestimme λ und μ so, dass der Verbindungsvektor senkrecht zu g und senkrecht zu h steht:
Das Skalarprodukt mit den beiden Richtungsvektoren
und
ergibt in diesem Fall jeweils den Wert 0.
u
| g |
u
| h |
| = | 0 |
| = | 0 |
| = |
| ausmultiplizieren | |||||||||||||||||||||||||||||||||||||||||||
| = |
| zusammenfassen | |||||||||||||||||||||||||||||||||||||||||||
| = |
| Gleichung I | |||||||||||||||||||||||||||||||||||||||||||
| = | 0 |
| = | 0 |
| = |
| ausmultiplizieren | |||||||||||||||||||||||||||||||||||||||||||
| = |
| zusammenfassen | |||||||||||||||||||||||||||||||||||||||||||
| = |
| Gleichung II | |||||||||||||||||||||||||||||||||||||||||||
Gleichung I und II bilden ein Gleichungssystem, das mit dem GTR gelöst werden kann.
Wer es lieber zu Fuß löst, kann z.B. Gleichung I nach auflösen und in Gleichung II einsetzen. Das ergibt:
μ
μ | = |
|
| = |
| Gleichung II | |||||||||||||||||
| = |
| zusammenfassen | |||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| :57 | |||||||||||||||||
| = |
| ||||||||||||||||||
Eingesetzt in Gleichung Ia:
| = |
|
3. Schritt: Länge des senkrechten Verbindungsvektors:
Setzt man die berechneten Werte von λ und μ beim Vektor
ein, so erhält man denjenigen Vektor
, der auf beiden Geraden g und h senkrecht steht. Es ergibt sich:
|
|
PQ
| = |
|
Damit ergibt sich als Abstand der beiden windschiefen Geraden g und h:
| = |
|
Wir erhalten erwartungsgemäß das selbe Ergebnis wie oben. Der Abstand der beiden windschiefen Geraden beträgt
LE.
|
Zugegeben: Die Rechnung war in diesem Fall aufwändiger als die erste Lösungsmöglichkeit, aber sie funktioniert...

Lernvideo
Koordinatengeometrie im Raum, Abstand windschiefer Geraden, Beispiel
Kanal: Mathegym

Lernvideo
Abstand windschiefer Geraden bestimmen
Kanal: MathemaTrick
Siehe auch