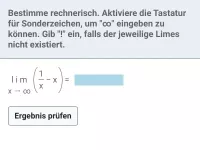
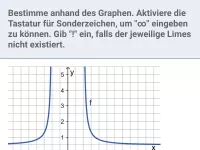
Was bedeutet es, wenn "f(x) für x → ∞ gegen c konvergiert" in der Mathematik?
Wenn f(x) für x → ∞ gegen c konvergiert, so bedeutet dies, dass |f(x) − c| kleiner als jede noch so winzige positive Zahl ε ist - wenn x nur groß genug gewählt wird.
Wie groß x dafür sein muss, ermittelt man mit Hilfe der Ungleichung
|f(x) − c| < ε
Beispiel
f(x) | = |
|
Ermittle den Grenzwert c für
und ermittle das maximale Intervall ]?;∞[, in dem sich f(x) und c um weniger als 0,05 unterscheiden.
| ∞ |
- Grenzwert ermitteln
| = |
|
Erläuterung: wenn der Nenner des Bruchterms immer größer wird, strebt der Wert des Bruchterms gegen 0.
Der ermittelte Grenzwert entspricht der horizontalen Asymptote mit der Gleichung
(siehe Skizze).
y | = |
|
- Graphische Interpretation
"f(x) und
unterscheiden sich um weniger als 0,05" kann auch so ausgedrückt werden:
− | 4 |
| 0,05 |
Graphisch interpretiert:
G | f |
| = | 0,1 |
y | = |
|
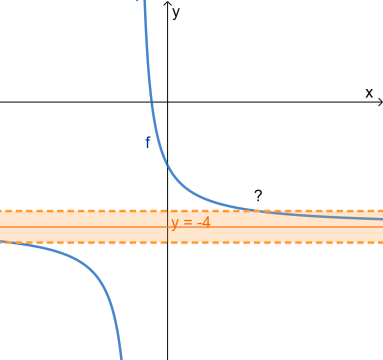
- Eintauchstelle ermitteln
Gesucht ist die in der Skizze mit "?" markierte Stelle, an der
für immer in den 0,1 breiten Streifen mit Symmetrieachse
eintaucht.
G | f |
y | = |
|
| = |
| ||||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| X | |||||||||||||||||
| = |
| ||||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
|
| |||||||||||||||||
| = |
| ||||||||||||||||||
Für
befindet sich
im Inneren des entsprechenden Streifens.
|
|
G | f |
Siehe auch