Wie kann man den Limes von f(x) für x → ∞ bzw. x → -∞ bestimmen?
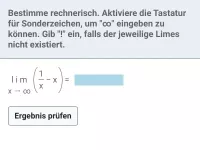
Ist der Funktionsterm f(x) gegeben, lässt sich der Limes von f(x) für x → ∞ bzw. x → -∞ auf verschiedene Arten ermitteln; am Beispiel f(x) = 1/x:
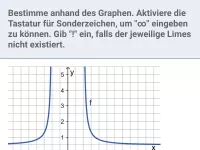
- indem man den Graphen skizziert; hier ergibt sich die bekannte Hyperbel mit der x-Achse als waagrechte Asymptote, also geht 1/x gegen 0.
- durch Überlegung, hier die Überlegung "ein Bruch mit festem Zähler wird (vom Betrag her) beliebig klein, wenn der Nenner nur groß genug ist".
- mit Hilfe einer Wertetabelle, z.B. setzt man hier in den Term 1/x der Reihe nach die x-Werte 10; 100; 1000; 10 000 (stellvertretend für x → ∞) ein und stellt fest, dass sich die entsprechenden y-Werte 0,1; 0,01; 0,001; 0,0001 immer weniger von 0 unterscheiden.
Siehe auch