Was versteht man unter den Wahrscheinlichkeiten P(A ∩ B), P_A(B) und P_B(A), wo treten sie im Baumdiagramm auf und wie berechnet man sie?

Unterscheide sorgfältig zwischen
  • P(A ∩ B)
    = Wahrscheinlichkeit, dass A und B eintritt; im Baumdiagramm steht sie am Ende des A - B - bzw. B - A - Pfades.

  • PA(B)
    = Wahrscheinlichkeit von Ereignis B unter der Bedingung, dass auch A eintritt (eingetreten ist); im Baumdiagramm steht sie über dem Ast, der von A zu B führt.
    = P(A ∩ B) / P(A)

  • PB(A)
    = Wahrscheinlichkeit von Ereignis A unter der Bedingung, dass auch B eintritt (eingetreten ist); im Baumdiagramm steht sie über dem Ast, der von B zu A führt.
    = P(A ∩ B) / P(B)
Beispiel
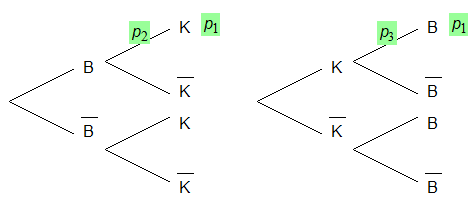
Betrachte die Ereignisse B = "Person trägt Brille" und K = "Person ist kurzsichtig". Drücke mit Worten aus und markiere in einem Baumdiagramm:
P
 
B ∩ K
 
    
 
P
B
 
K
 
    
 
P
K
 
B
Lösung:
P
 
B ∩ K
=
P
 
K ∩ B
=
P
 
"Person trägt Brille und ist kurzsichtig"
=
p
1
P
B
 
K
=
P
 
"Brillenträger ist kurzichtig"
=
p
2
P
K
 
B
=
P
 
"Kurzsichtiger trägt Brille"
=
p
3
graphik
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen