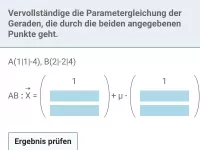
Wie bestimmt man die Oktanten, durch die eine Gerade im dreidimensionalen Koordinatensystem verläuft?
Um zu ermitteln, durch welche Oktanten eine Gerade verläuft, sollten zunächst die Spurpunkte (Schnittpunkte mit den Koordinatenebenen) bestimmt werden.
Beispiel
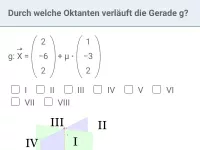
Durch welche Oktanten verläuft die Gerade g:
?
X
| = |
|
Lösung: Man bestimmt die Spurpunkte, also die Schnittpunkte der Geraden g mit den Koordinatenebenen, und erhält:
| = |
|
| = |
|
| = |
|
Erläuterung: den Schnittpunkt mit der
-Achse bestimmt man, indem man in der Parameterform von g die dritte Zeile gleich null setzt und nach μ auflöst (
). Dies eingesetzt in die ersten beiden Zeilen liefert die Koordinaten des Spurpunkts. Bei den anderen Spurpunkten analog, ausführlicher im Video.
x | 1,2 |
| = | 0,5 |
In folgender Skizze der acht Oktanten sind die errechneten Spurpunkte markiert (nicht maßstabsgetreu).
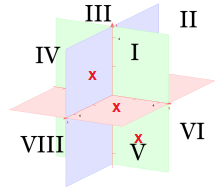
Nun lässt sich leicht ablesen, dass die Gerade g durch den 1., 4., 5. und 6. Oktanten geht.

Lernvideo
Geraden im Raum, Verlauf durch Oktanten anhand der Spurpunkte, Beispiel
Kanal: Mathegym
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie stellt man eine Gerade durch zwei Punkte A und B in Parameterform dar?
- Wie prüft man, ob ein Punkt P auf einer Geraden g in Parameterform liegt?
- Wie bestimmt man die Spurpunkte einer Geraden in Parameterform?
- Welche besonderen Lagebeziehungen zwischen einer Geraden und dem Koordinatensystem sind möglich und welche Rolle spielen dabei der Stützvektor und der Richtungsvektor?