Wie prüft man, ob ein Punkt P auf einer Geraden g in Parameterform liegt?
Gegeben ist die Gerade g. \[ g: \vec{X} = \begin{pmatrix} 1 \\ -1 \\ 5 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 4 \\ 2 \end{pmatrix} \]
Prüfe, ob die Punkte \( P(-1|3|5) \) und \( Q(10|-13|-1) \) auf \( g \) liegen.
Lösung:
- P ∈ g?
\[ \begin{pmatrix} -1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \\ 5 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 4 \\ 2 \end{pmatrix} \] \[ \begin{pmatrix} -2 \\ 4 \\ 0 \end{pmatrix} = \mu \cdot \begin{pmatrix} -3 \\ 4 \\ 2 \end{pmatrix} \]
Aus der zweiten Zeile folgt \( \mu = 1 \); aus der dritten Zeile dagegen \( \mu = 0 \). Es gibt also keine (übereinstimmende) Lösung für \( \mu \) und damit liegt P nicht auf \( g \).
- Q ∈ g?
\[ \begin{pmatrix} 10 \\ -13 \\ -1 \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \\ 5 \end{pmatrix} + \mu \cdot \begin{pmatrix} -3 \\ 4 \\ 2 \end{pmatrix} \] \[ \begin{pmatrix} 9 \\ -12 \\ -6 \end{pmatrix} = \mu \cdot \begin{pmatrix} -3 \\ 4 \\ 2 \end{pmatrix} \]
Aus der ersten Zeile folgt \( \mu = -3 \); aus der zweiten und dritten Zeile ebenso. Damit liegt Q auf \( g \).
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
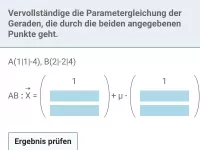
- Wie stellt man eine Gerade durch zwei Punkte A und B in Parameterform dar?
- Wie bestimmt man die Spurpunkte einer Geraden in Parameterform?
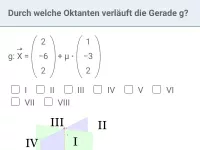
- Wie bestimmt man die Oktanten, durch die eine Gerade im dreidimensionalen Koordinatensystem verläuft?
- Welche besonderen Lagebeziehungen zwischen einer Geraden und dem Koordinatensystem sind möglich und welche Rolle spielen dabei der Stützvektor und der Richtungsvektor?