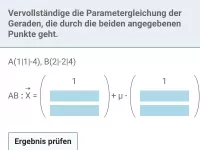
Wie stellt man eine Gerade durch zwei Punkte A und B in Parameterform dar?
Um die Gerade g durch die Punkte A und B in Parameterform darzustellen, kann man z.B.
- A oder B als Aufpunkt und
- den Verbindungsvektor von A nach B als Richtungsvektor verwenden.
Beispiel
Gib die Gerade g = AB in Parameterform an mit A(1|-1|2) und B(-2|5|5).
Lösung:
 |
|
Als fester Punkt auf g ("Aufpunkt") kann A oder B verwendet werden, als Richtungsvektor eignet sich der Verbindungsvektor von A nach B, also
| = |
|
Damit wird g z.B. durch folgende Gleichung in Parameterform beschrieben:
| = |
|
Oder, noch eleganter:
|
- - - - - - - - - - - - - - - - - - - - - - - - - - - -Erläuterungen:
(1) Üblicher Weise wählt man einen Richtungsvektor mit möglichst einfachen Koordinaten, darum wurde unten in der eleganteren Lösung der Richtungsvektor
| = |
|
gewählt, der ebenfalls parallel zu AB, aber nur ein Drittel mal so lang wie der Verbindungsvektor von A und B ist.
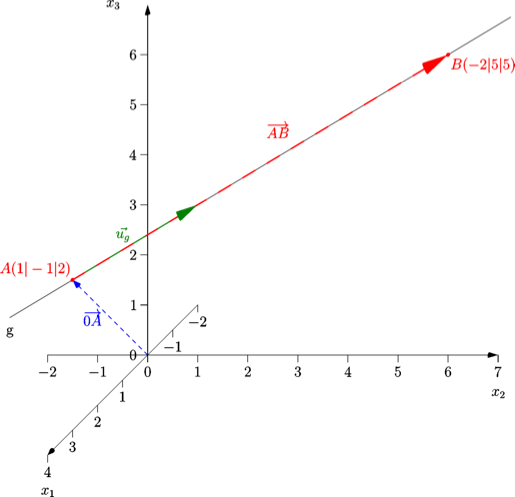
(2) Zur Verdeutlichung hier auch noch eine genaue Zeichnung der Geraden:
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie prüft man, ob ein Punkt P auf einer Geraden g in Parameterform liegt?
- Wie bestimmt man die Spurpunkte einer Geraden in Parameterform?
- Wie bestimmt man die Oktanten, durch die eine Gerade im dreidimensionalen Koordinatensystem verläuft?
- Welche besonderen Lagebeziehungen zwischen einer Geraden und dem Koordinatensystem sind möglich und welche Rolle spielen dabei der Stützvektor und der Richtungsvektor?