Wie bestimmt man die Spurpunkte einer Geraden in Parameterform?
Um den evtl. Schnittpunkt (Spurpunkt) einer Geraden mit der x1x2-Ebene zu bestimmen, muss man innerhalb der Geradengleichung (Parameterform) x3 = 0 setzen.
Entsprechend setzt man x1 = 0, um den Schnittpunkt mit der x2x3-Ebene zu bestimmen und x2 = 0 für den Schnittpunkt mit der x1x3-Ebene.
Beispiel
| = |
|
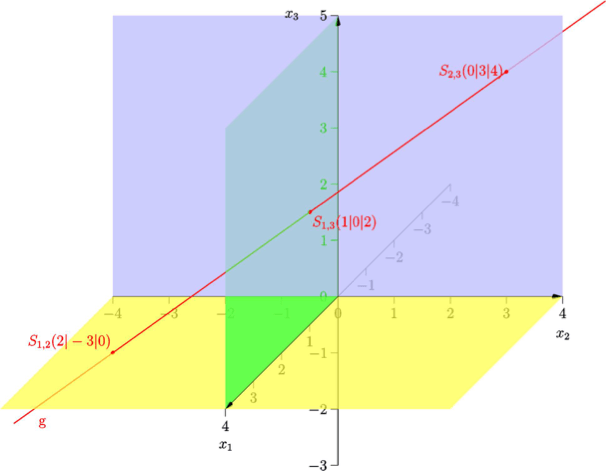
Bestimme sämtliche Schnittpunkte mit den Koordinatenebenen.
Lösung:
- Schnittpunkt mit der x1x2-Ebene
| = |
| |||||||||
| = |
| |||||||||
| = |
| |||||||||
Setzt man diesen μ-Wert in g ein, so ergibt sich als Schnittpunkt:
|
- Schnittpunkt mit der x1x3-Ebene
| = |
| |||||||||||
| = |
| |||||||||||
| = |
| |||||||||||
Setzt man diesen μ-Wert in g ein, so ergibt sich als Schnittpunkt:
|
- Schnittpunkt mit der x2x3-Ebene
| = |
| ||||||
| = |
| ||||||
| = |
| ||||||
Setzt man diesen μ-Wert in g ein, so ergibt sich als Schnittpunkt:
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie stellt man eine Gerade durch zwei Punkte A und B in Parameterform dar?
- Wie prüft man, ob ein Punkt P auf einer Geraden g in Parameterform liegt?
- Wie bestimmt man die Oktanten, durch die eine Gerade im dreidimensionalen Koordinatensystem verläuft?
- Welche besonderen Lagebeziehungen zwischen einer Geraden und dem Koordinatensystem sind möglich und welche Rolle spielen dabei der Stützvektor und der Richtungsvektor?