Was ist eine Ortskurve und wie bestimmt man ihre Gleichung?

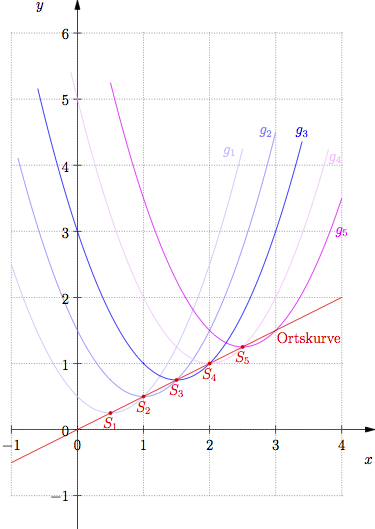
Eine Kurve, auf der alle Punkte einer Funktionenschar liegen, die eine bestimmte Eigenschaft erfüllen, wird als Ortskurve bezeichnet.

Sind die Koordinaten der betrachteten Punkte (z.B. Hoch- oder Tiefpunkte) in Abhängigkeit von einem Parameter a gegeben, erhält man die Gleichung der Ortskurve in zwei Schritten:

  • Auflösen der x-Koordinatengleichung nach a
  • Einsetzen in die y-Koordinatengleichung
Beispiel
Bestimme die Ortskurve der Scheitelpunkte der Funktionenscharen
f
a
x
=
x
2
+
a und
g
a
x
=
x
2
−
ax
+
1
4
 
a
2
+
1
4
 
a
Die Funktionenschar f
a
x
=
x
2
+
a
 
beschreibt die um a nach oben bzw. unten verschobenen Normalparabel.
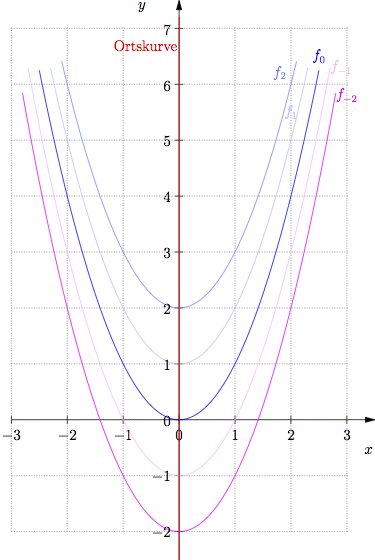
Die Scheitelpunkte bewegen sich auf der Senkrechten mit der Gleichung x=0.
graphik
- - - - - - - - -
g
a
x
=
x
2
−
ax
+
1
4
 
a
2
+
1
4
 
a
g
a
'
 
x
=
2
 
x
−
a
  • 1. Schritt
Bestimmung der x-Koordinate des Scheitelpunktes (Tiefpunkt): Nullstelle der Ableitung bestimmen
2x
−
a
=
0
+
a
2x
=
a
:
2
x
=
1
2
 
a
  • 2. Schritt
Bestimmung der y-Koordinate des Scheitels: x in die Funktionsgleichung einsetzen
g
a
1
2
 
a
=
1
2
 
a
2
−
a
·
1
2
 
a
+
1
4
 
a
2
+
1
4
 
a
=
1
4
 
a
2
−
1
2
 
a
2
+
1
4
 
a
2
+
1
4
 
a
=
1
4
 
a
Die Scheitelpunkte der Funktionenschar haben die Koordinaten
 
S
a
1
2
 
a
 
|
 
1
4
 
a
  • 3. Schritt
Gleichung der Ortskurve aller Scheitel berechnen
Für die Gleichung der Ortskurve muss die x-Koordinate der Scheitelpunkte nach a aufgelöst werden.
x
=
1
2
 
a
·
2
2x
=
a
a
=
2
 
x
Das Ergebnis wird in die y-Koordinate der Scheitelpunkte eingesetzt.
y
=
1
4
·
a
a einsetzen
y
=
1
4
·
2x
y
=
1
2
 
x
Die Gleichung der Ortskurve lautet
:
y
=
1
2
 
x
graphik
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen