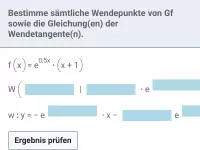
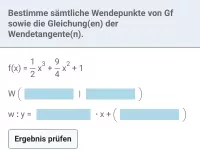
Wie bestimmt man den Funktionsterm einer Polynomfunktion n-ten Grades anhand gegebener Grapheneigenschaften?
Eine ganzrationale Funktion n-ten Grades besitzt n+1 Unbekannte. Zur eindeutigen Bestimmung der Funktionsgleichung wird ein Gleichungssystem benötigt, das n+1 Gleichungen enthält.
Vorgehensweise, um die Funktionsgleichung zu bestimmen:
- Schreibe die allgemeine Funktionsgleichung mit ihren Ableitungen auf.
- "Übersetze" alle gegebenen Eigenschaften in mathematische Gleichungen.
- Stelle das Gleichungssystem auf, indem du die Koordinaten in die gefundenen Gleichungen einsetzt.
- Löse das Gleichungssystem
- Setze die gefundene Lösung in die Funktionsgleichung ein
Beispiel 1
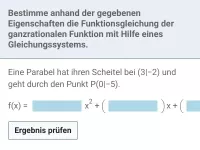
Eine Funktion 2. Grades hat einen Tiefpunkt bei (0|1) und geht durch den Punkt P(2|9).
f(x) | = |
|
1. allgemeine Funktionsgleichung
| = |
| |||||||||||
| = |
| |||||||||||
2. Eigenschaften ausnutzen, um drei Gleichungen zu erhalten
I: f(0)=1, da (0|1) ein Punkt auf dem Funktionsgraphen ist
II: f'(0)=0, da an der Stelle x=0 ein Tiefpunkt ist
III: f(2)=9, da P(2|9) Punkt auf dem Funktionsgraphen ist
3. Werte einsetzen, Gleichungssystem aufstellen:
| = |
| ||||||||||||||||||||
| = |
| ||||||||||||||||||||
| = |
| ||||||||||||
| = |
| ||||||||||||
| = |
| ||||||||||||||||||||
| = |
| ||||||||||||||||||||
4. Gleichungssystem lösen:
Die Lösungen für b und c lassen sich ablesen: b=0, c=1.
Setzt man dies nun in die dritte Gleichung ein, erhält man a:
| = |
|
| |||||||||||||
| = |
|
| |||||||||||||
|
5. Zusammen ergibt sich die gesuchte Funktionsgleichung:
|
In den folgenden Videos werden ähnliche Aufgaben behandelt.

Lernvideo
Bestimmung einer ganzrationalen Funktion anhand von Eigenschaften
Kanal: Mathegym
Lernvideo
STECKBRIEFAUFGABEN Mathe – Ganzrationale Funktionen bestimmen 3. Grades
Kanal: MathemaTrick
Beispiel 2
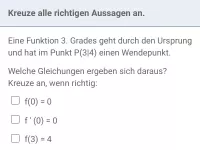
Eine Funktion 4. Grades hat verläuft durch den Ursprung und besitzt in H(2|3) einen Hochpunkt, in T(4|-2) einen Tiefpunkt. Reicht die gegebene Information aus, um die Gleichung der ganzrationalen Funktion eindeutig zu bestimmen?
Lösung: Die allgemeine Funktionsgleichung einer Funktion 4. Grades hat fünf Parameter a, b, c, d und e:
f(x) | = |
|
Daher werden FÜNF Gleichungen benötigt, um die Parameter a bis e zu ermitteln. Es gilt:
- Jeder Punkt, der auf dem Funktionsgraphen liegt, liefert mindestens eine Gleichung, denn seine Koordinaten erfüllen die Funktionsgleichung. Beispiel: Liegt P(2|8) auf dem Graphen von f(x), so gilt: f(2)=8
- Jeder besondere Punkt liefert sogar zwei Gleichungen für das Gleichungssystem, weil die Besonderheit etwas über die erste oder zweite Ableitung an der Stelle aussagt. Beispiel: Ist T(1|5) ein Wendepunkt der Funktion f(x), so gilt: f(1)=5 und f''(1)=0
Die angegebene Information reicht aus, da wir folgende fünf Gleichungen aufstellen können:
| = |
| da durch den Ursprung | ||||
| = |
| da durch (2|3) | ||||
| = |
| da Hochpunkt an dieser Stelle | ||||
| = |
| da durch (4|-2) | ||||
| = |
| da Tiefpunkt an dieser Stelle | ||||
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff + Video
Bestimmung ganzrationaler Funktionen
Bestimmung ganzrationaler Funktionen aufgrund vorgegebener Eigenschaften -
≈Oberstufe - Aufgaben + Stoff + Video
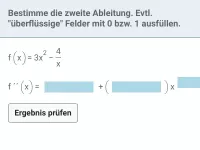
Zweite Ableitung/Krümmung/Wendepunkt
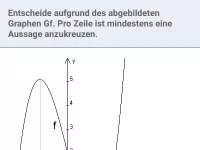
Bestimmung der lokalen Krümmung eines Graphen / maximaler Krümungsintervalle / relativer Extrema mit Hilfe der zweiten Ableitung. Zusammenhang der Graphen von f, f´und f ´´. Bestimmung von Wendepunkten und Wendetangenten.
Ähnliche Themen
- Wie erhält man die zweite Ableitung f´´ und unter welchen Bedingungen existiert sie?
- Wie beeinflussen die Vorzeichen von f´ und f´´ den Graphenverlauf von f?
- Wie bestimmt man die Krümmungsintervalle eines Funktionsgraphen?
- Wie kann man mit der zweiten Ableitung feststellen, ob an einer Nullstelle der ersten Ableitung ein relatives Extremum vorliegt und welcher Art es ist?
- Was ist ein Wendepunkt und wie bestimmt man ihn rechnerisch?