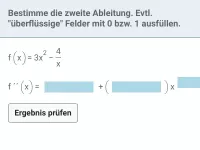
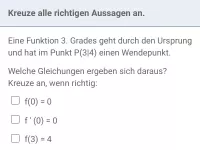
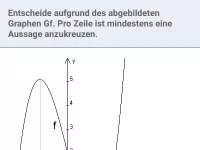
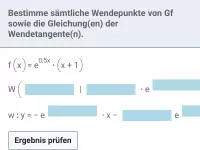
Wie kann man mit der zweiten Ableitung feststellen, ob an einer Nullstelle der ersten Ableitung ein relatives Extremum vorliegt und welcher Art es ist?
Sei a eine Nullstelle der ersten Ableitung, also f ´(a) = 0. Dann gilt:
f ´´ (a ) < 0 ⇒ relatives Maximum bei x = a
f ´´ (a ) > 0 ⇒ relatives Minimum bei x = a
Vorsicht: Aus f ´´ (a) = 0 folgt NICHT, dass kein relatives Extremum vorliegt. Überprüfe in diesem Fall f ´ auf Vorzeichenwechsel an der Nullstelle x = a. Zur Erinnerung:VZW +/- von f ´ ⇔ relatives Maximum
VZW -/+ von f ´ ⇔ relatives Minimum
kein VZW von f´ ⇔ Terrassenpunkt
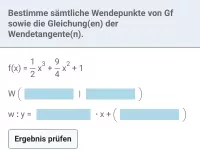
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie erhält man die zweite Ableitung f´´ und unter welchen Bedingungen existiert sie?
- Wie beeinflussen die Vorzeichen von f´ und f´´ den Graphenverlauf von f?
- Wie bestimmt man die Krümmungsintervalle eines Funktionsgraphen?
- Wie bestimmt man den Funktionsterm einer Polynomfunktion n-ten Grades anhand gegebener Grapheneigenschaften?