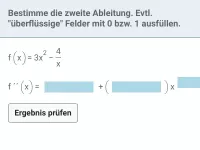
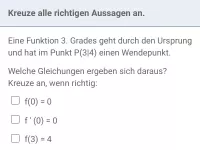
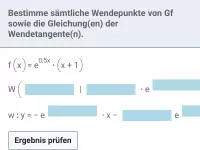
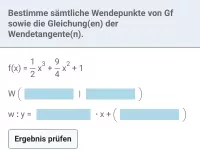
Wie beeinflussen die Vorzeichen von f´ und f´´ den Graphenverlauf von f?
| f bzw Gf | f ´ | f ´´ |
| streng monoton zunehmend | positiv | |
| streng monoton abnehmend | negativ | |
| linksgekrümmt | streng monoton zunehmend | positiv |
| rechtsgekrümmt | streng monoton abnehmend | negativ |
Beispiel
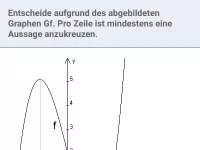
Lies das jeweilige Vorzeichen von \( f(-1) \), \( f'(-1) \) und \( f''(-1) \) ab. Gib jeweils ein möglichst großes Intervall an (geschätzt), in dem \( f \), \( f' \) bzw. \( f'' \) positiv ist.
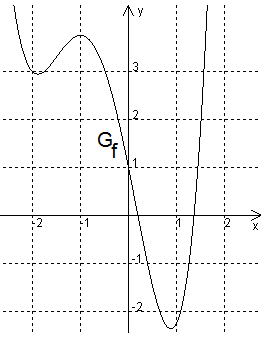
Lösung:
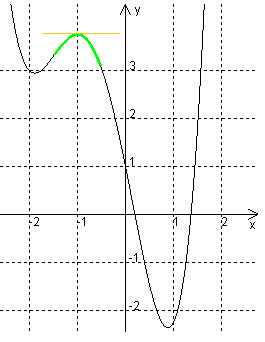
\( f(-1) > 0 \) [Graph über x-Achse].
\( f'(-1) = 0 \) [waagrechte Tangente, also keine Steigung (orange)].
\( f''(-1) < 0 \) [Rechtskrümmung (grün)].
Geschätzte Intervalle:
\( f(x) > 0 \) für \( x \in \left]-\infty; 0,2\right[ \) (d.h. Graph hier oberhalb der x-Achse)
\( f'(x) > 0 \) für \( x \in \left]0,9; \infty\right[ \) (d.h. Graph hier streng monoton steigend)
\( f''(x) > 0 \) für \( x \in \left]-\infty; -1,3\right[ \) (d.h. Graph hier linksgekrümmt)
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie erhält man die zweite Ableitung f´´ und unter welchen Bedingungen existiert sie?
- Wie bestimmt man die Krümmungsintervalle eines Funktionsgraphen?
- Wie kann man mit der zweiten Ableitung feststellen, ob an einer Nullstelle der ersten Ableitung ein relatives Extremum vorliegt und welcher Art es ist?
- Wie bestimmt man den Funktionsterm einer Polynomfunktion n-ten Grades anhand gegebener Grapheneigenschaften?