Wie bestimmt man die Krümmungsintervalle eines Funktionsgraphen?
Die Krümmungsintervalle einer zweimal differenzierbaren Funktion ermittelt man mit Hilfe einer Vorzeichenuntersuchung von f ´´. Bestimme dazu zunächst die Nullstellen von f ´´.
Beispiel 1
Bestimme das Krümmungsverhalten der Funktion
| = |
|
Lösung
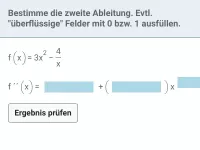
- f '' bestimmen
| = |
|
| = |
|
- f '' (x) = 0
| = |
| MNF | |||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||||||||
- Maximale Krümmungsintervalle
|
|
|
|
|
|
| |||||||||||||||||||||
|
|
|
|
|
| |||||||||||||||||||||
|
|
|
|
|
|
Erläuterung: auf die Vorzeichen der zweiten Ableitung kommt man
- z.B. durch Einsetzen von jeweils einem x-Wert aus jedem der Intervalle in die zweite Ableitung.
- Eleganter ist es, wenn man sich hier den quadratischen Term der zweiten Ableitung als nach oben geöffnete Parabel vorstellt. Dann ist sofort klar: die Parabel ist - von links nach rechts - erst über, dann unter, dann wieder über der x-Achse, daher der Vorzeichenverlauf Plus-Minus-Plus.
Beispiel 2
| = |
|
Lösung:
- f '' bestimmen
| = |
|
| = |
|
- f ''(x) = 0
| = |
|
| ||||||||||||||||||||||||||||||||||||
| = |
|
| ||||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||||||||||||||
- Maximale Krümmungsintervalle
|
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
| |||||||||||||||||
|
|
|
|
|
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie erhält man die zweite Ableitung f´´ und unter welchen Bedingungen existiert sie?
- Wie beeinflussen die Vorzeichen von f´ und f´´ den Graphenverlauf von f?
- Wie kann man mit der zweiten Ableitung feststellen, ob an einer Nullstelle der ersten Ableitung ein relatives Extremum vorliegt und welcher Art es ist?
- Was ist ein Wendepunkt und wie bestimmt man ihn rechnerisch?
- Wie bestimmt man den Funktionsterm einer Polynomfunktion n-ten Grades anhand gegebener Grapheneigenschaften?