Wie bestimmt man die Funktionsgleichung einer Tangentenschar zu einem Funktionsgraphen?
Die Schar aller Tangenten an einen Funktionsgraphen im Punkt (a|f(a)) kann durch eine Funktionsgeichung angegeben werden. Zur Ermittlung dieser Funktionsgleichung geht man genauso vor wie bei einer einzelnen Tangente. Der einzige Unterschied besteht darin, dass man mit allgemeinen Koordinaten a und f(a) rechnen muss statt mit festen Werten.
Beispiel
| = |
|
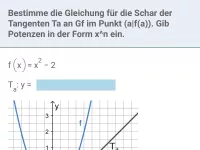
Bestimme die Gleichung für die Schar der Tangenten
an
im Punkt (a|f(a)).
T | a |
G | f |
| = |
|
| = |
|
| = |
|
Die Tangente
an
im Punkt
hat die Steigung
Damit kann die Gleichung der Schar bestimmt werden:
T | a |
G | f |
| ) |
| − | 2. |
| = |
|
Nach Einsetzen der Koordinaten des Berührpunkts erhält man die untere Gleichung, die nach t (y-Achsenabschnitt) aufgelöst werden kann:
| = |
| Punktkoordinaten einsetzen | |||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||
| = |
|
| |||||||||||||||||||||||||
| = |
| ||||||||||||||||||||||||||
|
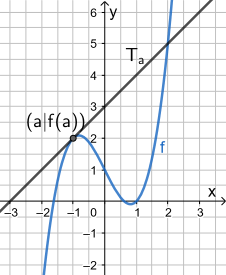
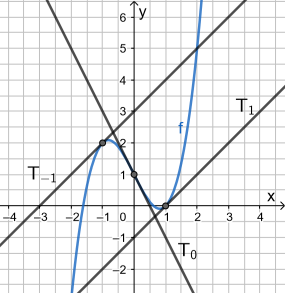
Zur Illustration sind hier drei Tangenten der Schar abgebildet:
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff + Video
Funktionenschar
Eigenschaften von Funktionenscharen in Abhängigkeit vom Scharparameter -
≈Oberstufe - Aufgaben + Stoff + Video
Tangentengleichung und Steigungswinkel
Bestimmung des Steigungswinkels einer Tangente/Normalen an einer vorgegebenen Stelle; Bestimmung der Tangente an einer vorgegebenen Stelle des Graphen bzw. mit vorgegebenen Eigenschaften (Steigung, Steigungswinkel); Bestimmung des Berührpunkts der Tangente, die durch einen bestimmten Punkt geht
Ähnliche Themen
- Wie bestimmt man die Steigung der Tangente an einem Punkt eines Graphen?
- Wie bestimmt man den Funktionsterm einer Polynomfunktion n-ten Grades anhand gegebener Grapheneigenschaften?
- Was ist eine Funktionenschar und wie berechnet man sie?
- Was ist eine Ortskurve und wie bestimmt man ihre Gleichung?
- Wie ist der Steigungswinkel einer Geraden definiert und wie hängt er mit der Steigung m zusammen?
- Was ist die Normale eines Funktionsgraphen an einem Punkt und wie berechnet man ihre Steigung?
- Wie bestimmt man den Parameterwert k für den Graphen einer Funktionenschar?