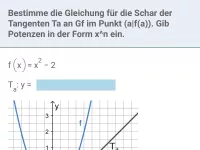
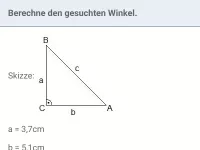
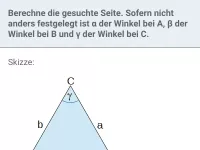
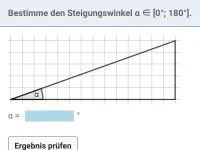
Wie ist der Steigungswinkel einer Geraden definiert und wie hängt er mit der Steigung m zusammen?
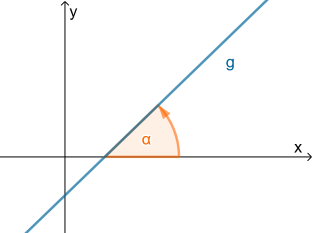
Der Steigungswinkel 0°≤α<180° einer Geraden bezeichnet die Größe des Winkels, um den g gegenüber der x-Achse gedreht ist. Für 0°<α<90° handelt es sich um eine steigende, für 90°<α<180° um eine fallende Gerade.
Die Steigung m einer Geraden und ihr Steigungswinkel α stehen in folgendem Zusammenhang:m=tan(α)
Beachte: wenn m gegeben und α gesucht ist, rechnet man zunächst tan-1(m) aus. Ist das Ergbnis positiv, hat man damit α ermittelt. Ist es negativ, addiert man noch 180° hinzu.
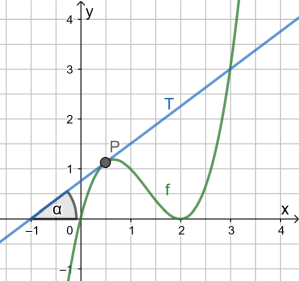
Beispiel 1
| = |
|
Berechne den Steigungswinkel der Tangente an
im Punkt P(0,5|?).
G | f |
Zunächst multipliziert man
aus, um die Ableitung nach Regel bilden zu können.
f |
|
| = |
| |||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||
| = |
| |||||||||||||||||||||||
Die Steigung der Tangente ergibt sich dann als
.
f ´ |
|
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
|
| = |
| ||||||||||||||||||||||||
Durch Umstellung der Formel
erhält man schließlich den Steigungswinkel.
m | = |
|
| = |
| einsetzen | |||||||||||||||||||
| = |
|
| |||||||||||||||||||
| = |
| ||||||||||||||||||||
Beispiel 2
Eine Straße weist eine 39%ige Steigung auf. Berechne den Steigungswinkel.
Lösung:
Stellt man sich die Straße als Abschnitt einer Geraden vor, so hat diese Gerade die Steigung
| = | 0,39. |
m | = |
|
0,39 | = |
|
α | = |
|
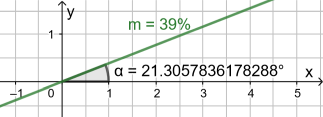
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈Oberstufe - Aufgaben + Stoff + Video
Tangentengleichung und Steigungswinkel
Bestimmung des Steigungswinkels einer Tangente/Normalen an einer vorgegebenen Stelle; Bestimmung der Tangente an einer vorgegebenen Stelle des Graphen bzw. mit vorgegebenen Eigenschaften (Steigung, Steigungswinkel); Bestimmung des Berührpunkts der Tangente, die durch einen bestimmten Punkt geht -
≈9. Klasse - Aufgaben + Stoff + Video
Trigonometrie am rechtwinkligen Dreieck
Berechnungen im rechtwinkligen Dreieck mit Hilfe von Sinus, Kosinus und Tangens; Steigungswinkel; Textaufgaben
Ähnliche Themen
- Wie lauten die Formeln für Sinus, Kosinus und Tangens im rechtwinkligen Dreieck?
- Wie bestimmt man die Steigung der Tangente an einem Punkt eines Graphen?
- Was ist die Normale eines Funktionsgraphen an einem Punkt und wie berechnet man ihre Steigung?
- Wie bestimmt man die Funktionsgleichung einer Tangentenschar zu einem Funktionsgraphen?