Was ist eine Funktionenschar und wie berechnet man sie?
Eine Funktionenschar ist gegeben durch eine Funktionsgleichung mit (mindestens) einem Parameter. Jeder Parameterwert liefert eine spezielle Funktion. Insofern ist durch die Gleichung der Funktionenschar eine Menge an Kurven gegeben.
Mit der Funktionsgleichung der Schar kann man rechnen wie mit einer Funktionsgleichung ohne Parameter (Punkt-Koordinaten einsetzen, ableiten, ...). Der Parameter wird dabei behandelt wie eine Zahl.
Beispiel 1
| = |
|
| = |
|
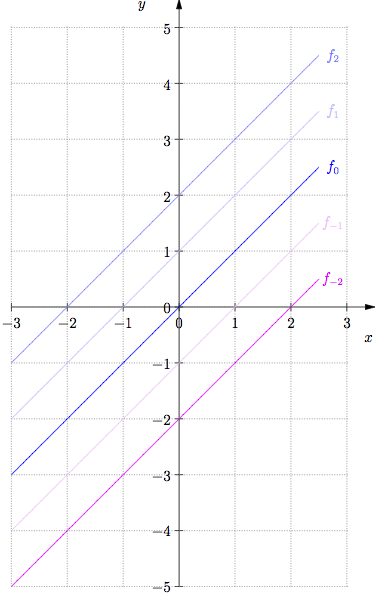
| = |
|
Beispiel 2
| = |
|
| = |
|
- Kandidaten für Extremwerte: Nullstellen der Ableitung bestimmen
| = |
| x ausklammern | |||||||||||
| = |
| Faktorregel | |||||||||||
Zur Erinnerung: ein Produkt ist Null genau dann, wenn einer der Faktoren Null ist.
| = | 0 |
| = |
|
| = |
|
- Zweite Ableitung bestimmen, um Art des Extremwerts festzulegen:
| = |
|
- Werte einsetzen:
| = |
|
| = | 2a |
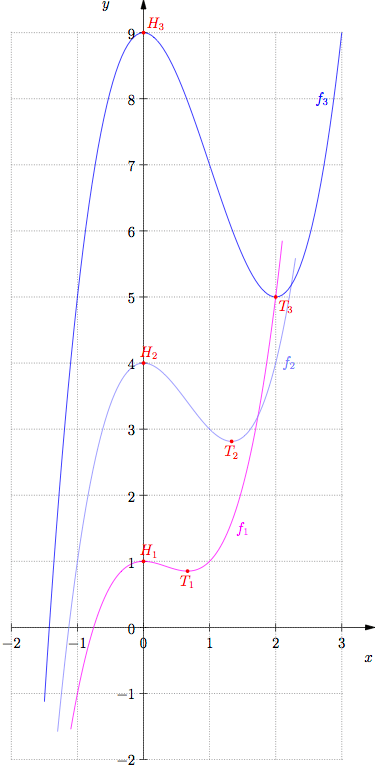
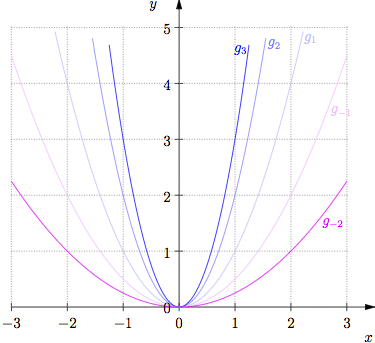
Für positive Werte von a ist fa '' (0) kleiner Null und fa '' (2/3a) größer Null. Damit liegt an der Stelle x=0 ein Maximum, an der Stelle x=2/3a ein Minimum vor. Im Bild unten sind die Funktionen für a=1, a=2 und a=3 gezeichnet.