Welche einzigartige Eigenschaft besitzen Punkte auf der Symmetrieachse bezüglich eines Punkts P und seines Spiegelpunkts P´?
Punkte, die auf der Symmetrieachse liegen, haben eine exklusive Eigenschaft (d.h. nur sie haben diese Eigenschaft): Sie sind zu symmetrischen Punkten gleich weit entfernt. D.h.
- sind P und P´ zueinander achsensymmetrische Punkte und A ein beliebiger Punkt der Achse, so ist dieser zu P und P´gleich weit entfernt.
- sind P und P´ zueinander achsensymmetrische Punkte und von A gleich weit entfernt, so muss A auf der Spiegelachse liegen.
Beispiel 1
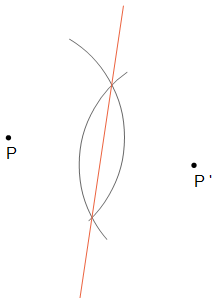
Gegeben sind die Punkte P und P'. Gesucht ist die Spiegelachse a, die P auf P' abbildet.

Lösung: Man zeichnet zwei gleich große Kreise um P und P', die sich schneiden. Diese Schnittpunkte haben jeweils von P und P' die gleiche Entfernung und müssen daher auf der Achse liegen.
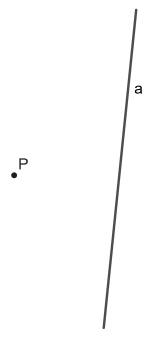
Beispiel 2
Der Punkt P soll an der Achse a gespiegelt werden.
Lösung: Man wählt zwei beliebige Achsenpunkte A und B (aus praktischen Gründen sollten sie nicht zu nah beieinander liegen). Dann zeichnet man um A und B jeweils einen Kreis durch P. Beide schneiden sich im Spiegelpunkt P'.
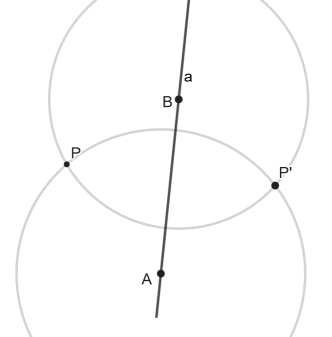
Begründung für dieses Vorgehen: P und P' haben von A und B jeweils dieselbe Entfernung. AB muss somit Spiegelachse bzgl. der Punkte P und P' sein.
Beispiel 3
Ein Winkel soll halbiert werden.
Lösung:
- Ziehe einen Kreis um den Scheitelpunkt, dieser schneide die beiden Schenkel in den Punkten A und B.
- Ziehe zwei gleich große Kreise um A und um B. Durch deren Schnittpunkt C verläuft die Winkelhalbierende.
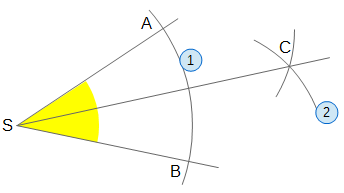
Begründung für das Vorgehen: S und C sind jeweils gleich weit von A und B entfernt. Damit ist SC Spiegelachse beider Schenkel.
Beispiel 4
(A) Von P aus soll ein Lot auf g gefällt werden (P ∉ g).
(B) Im Punkt P soll ein Lot zur Geraden g errichtet werden (P ∈ g).

Lösung zu (A):
- Wähle zwei Punkte A und B auf g.
- Ziehe um A und B jeweils einen Kreis durch P. Das Lot verläuft durch die Kreisschnittpunkte.
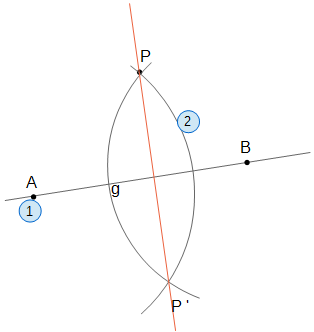
Begründung für das Vorgehen: Man spiegelt P an g. Die Strecke [PP´] steht somit senkrecht auf g.
Lösung zu (B):
- Ziehe einen Kreis um P, so dass dieser die Gerade g in zwei Punkten A und B schneidet.
- Ziehe zwei gleich große Kreise um A und um B. Durch deren Schnittpunkt C verläuft das Lot.
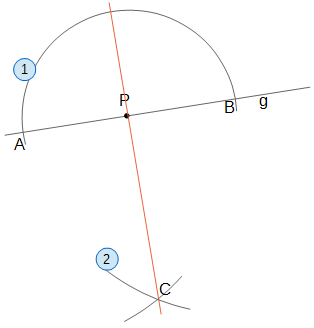
Begründung für das Vorgehen: Man konstruiert die Mittelsenkrechte von [AB]; diese geht durch P, da P der Mittelpunkt von [AB] ist.
Beispiel 5
(A) Von P aus soll ein Lot auf g gefällt werden (P ∉ g).

(B) Im Punkt P soll ein Lot zur Geraden g errichtet werden (P ∈ g).

Lösung zu (A):
- Wähle zwei Punkte A und B auf g.
- Ziehe um A und B jeweils einen Kreis durch P. Das Lot verläuft durch die Kreisschnittpunkte.

Begründung für das Vorgehen: man spiegelt P an g. Die Strecke
steht somit senkrecht auf g.
PP´
Lösung zu (B):
- Ziehe einen Kreis um P, so dass dieser die Gerade g in zwei Punkten A und B schneidet.
- Ziehe zwei gleich große Kreise um A und um B. Durch deren Schnittpunkt C verläuft das Lot.

Begründung für das Vorgehen: man konstruiert die Mittelsenkrechte von
; diese geht durch P, da P der Mittelpunkt von
ist.
AB
AB
Siehe auch