Wie kann ein quadratischer Term faktorisiert werden und welche Rolle spielen dabei die Lösungen der Nullgleichung?

Ein quadratischer Term (q · x² + r · x + s) kann evtl. als Produkt von zwei linearen Termen (linear ist z.B. x + 2) geschrieben werden. Dies hängt von den Lösungen der entsprechenden Nullgleichung (pq-Formel!) ab:
  • Zwei unterschiedliche Lösungen a und b: der Term zerfällt in q · (x − a) · (x − b).

  • Eine Lösung a: der Term zerfällt in q · (x − a)².

  • Keine Lösung ("Minus unter der Wurzel"): der Term ist nicht zerlegbar.
Beispiel
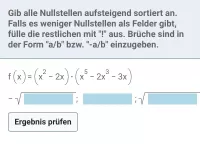
Zerlege, falls möglich, in Linearfaktoren:
a
 
   
 
−
2x
2
+
3x
+
2
b
 
   
 
−
3x
2
+
x
−
5
Lösung:
  • zu (a)
−
2x
2
+
3x
+
2
=
0
:
(-2)
x
2
−
3
2
 
x
−
1
=
0
pq
−
Formel
x
1,2
=
3
4
 
±
 
9
16
+
1
x
1,2
=
3
4
 
±
 
25
16
x
1,2
=
3
4
 
±
 
5
4
x
1
=
−
0,5
x
2
=
2
Die Zerlegung lautet damit:
−
2
 
x
2
+
3x
+
2
=
−
2
·
x
 
+
0,5
·
x
 
−
2
  • zu (b)
−
3x
2
+
x
−
5
=
0
:
(-3)
x
2
−
1
3
 
x
+
5
3
=
0
Diese Gleichung ist nicht lösbar, da die Diskriminante D (Term unter der Wurzel) negativ ist:
D
=
1
6
2
−
5
3
=
1
36
−
5
3
<
0
Damit ist eine Zerlegung in Linearfaktoren nicht möglich.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen