Was sind die fünf grundlegenden Potenzgesetze?

Potenzgesetze:
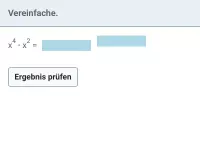
  1. Potenzen mit gleicher Basis werden multipliziert, indem man die Exponenten addiert und die Basis beibehält.
    ap · aq = ap + q

  2. Potenzen mit gleicher Basis werden dividiert, indem man die Exponenten subtrahiert und die Basis beibehält.
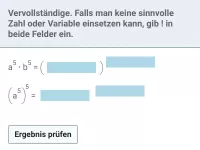
    ap : aq = ap − q

  3. Potenzen mit gleichen Exponenten werden multipliziert, indem man die Basen multipliziert und den Exponenten beibehält.
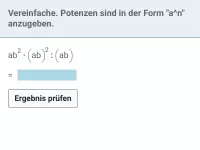
    aq · bq = (a · b)q

  4. Potenzen mit gleichen Exponenten werden dividiert, indem man die Basen dividiert und den Exponenten beibehält.
    aq : bq = (a : b)q

  5. Potenzen werden potenziert, indem man die Exponenten multipliziert.
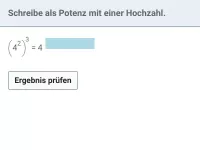
    (ap)q = ap·q
Beispiel 1
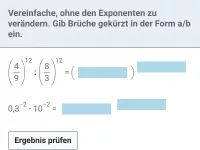
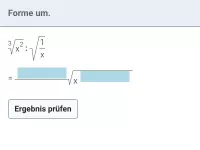
Forme, falls möglich, in EINE Wurzel um, in der nur noch positive Exponenten auftreten.
a)  
a
3
·
a
b)  
a
3
a
c)  
5
a
−
2
d)  
a
+
a
1,5
Zu a)
a
3
·
a
=
a
3
·
a
0,5
Exponenten addieren
=
a
3,5
=
a
7
2
=
a
7

Zu b)
a
3
a
=
a
1
a
1
3
Exponenten subtrahieren
=
a
2
3
=
3
a
2

Zu c)
5
a
−
2
=
a
1
5
−
2
Exponenten multiplizieren
=
a
−
2
5
=
1
a
2
5
=
5
1
a
2

Zu d)
a
 
+
 
a
1,5
=
?
Vorsicht: es handelt sich um eine Summe (Potenzgesetze gelten nicht für Summen und Differenzen), die beiden Summanden lassen sich also nicht zu einer Potenz zusammenfassen. Aber man kann ausklammern:
a
+
a
1,5
=
a
+
a
1
+
0,5
zweiten Summand als Produkt (Potenzgesetz rückwärts)
=
a
+
a
·
a
jetzt ausklammern
=
a
·
1
+
a
Potenzen und Wurzeln vereinfachen – Potenzen mit rationalen Exponenten (Klasse 10)
Lernvideo

Potenzen und Wurzeln vereinfachen – Potenzen mit rationalen Exponenten (Klasse 10)

Kanal: MathemaTrick
Wurzel in Wurzel auflösen – Terme vereinfachen mit Wurzeln
Lernvideo

Wurzel in Wurzel auflösen – Terme vereinfachen mit Wurzeln

Kanal: MathemaTrick
Beispiel 2
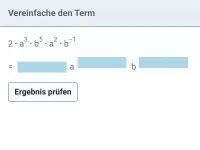
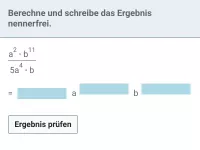
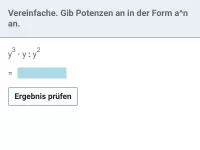
Fasse zusammen:
35c
7
6d
2
:
7
 
c
2
d
5
Lösung:
35c
7
6d
2
:
7
 
c
2
d
5
=
35c
7
6d
2
·
7c
2
d
5
alles auf einen Bruchstrich
=
5c
7
6
 
d
7
·
c
2
d-Potenzen multipliziert durch Addition der Exponenten, außerdem mit 7 gekürzt
=
5
 
c
5
6
 
d
7
c-Potenzen dividiert durch Subtraktion der Exponenten
=
5
6
 
c
5
 
d
−
7
d-Potenz nicht mehr im Nenner, dafür mit negativem Exponent
Ein noch schwierigeres Beispiel in folgendem Video
:
Terme mit POTENZEN zusammenfassen – Terme vereinfachen einfach erklärt
Lernvideo

Terme mit POTENZEN zusammenfassen – Terme vereinfachen einfach erklärt

Kanal: MathemaTrick
Beispiel 3
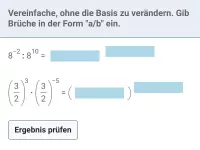
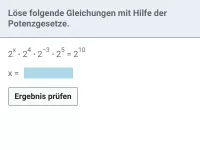
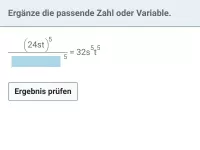
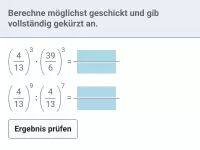
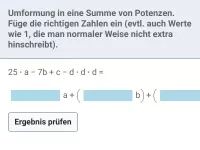
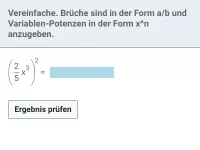
Fasse jeweils zusammen:
(a)
 
6
7
:
6
3
(b)
 
2
5
:
6
5
Zu (a)
Da die Potenzen dieselbe Basis haben, subtrahiert man die Exponenten:
6
7
:
6
3
=
6
7
−
3
=
6
4
=
6
2
·
6
2
=
6
·
6
=
36

Zu (b)
Da die Potenzen denselben Exponent haben, diviert man die Basen:
2
5
:
6
5
=
2
:
6
5
=
2
:
6
5
kürzen
=
1
3
5
Beispiel 4
Beispiel zu Potenzgesetz 1:
 
    
 
3
2
·
3
5
=
3
2
+
5
=
3
7
=
3
·
3
·
3
·
3
·
3
·
3
·
3
7mal
=
2187
Beispiel zu Potenzgesetz 2:
 
    
 
5
6
:
5
5
=
5
6
−
5
=
5
1
=
5
Beispiel zu Potenzgesetz 3:
 
    
 
5
2
·
7
2
=
5
·
7
2
=
35
2
=
1225
Beispiel zu Potenzgesetz 4:
 
    
 
15
2
:
5
2
=
15
:
5
2
=
3
2
=
9
Beispiel zu Potenzgesetz 5:
 
    
 
2
3
4
=
2
3
·
4
=
2
12
=
4096
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen