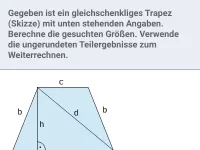
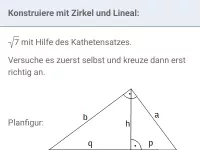
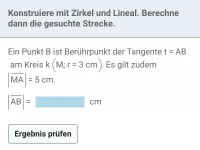
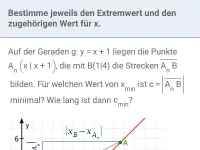
Wie löst man Extremwertaufgaben in vier Schritten?

Bei Extremwertaufgaben geht man am besten in folgenden Schritten vor:
  1. Darstellung der zu optimierenden Größe als Term
  2. Term in Abhängigkeit von x angeben
  3. Term umformen mithilfe der quadratischen Ergänzung.
  4. Extremwert und zugehöriges x ablesen.
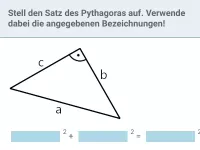
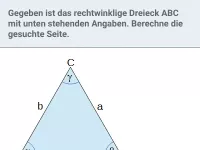
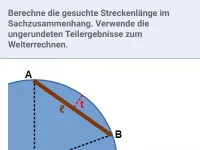
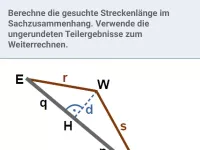
Beispiel
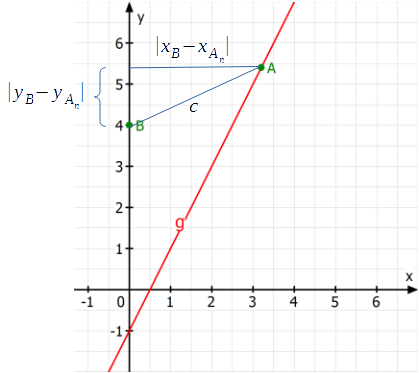
Auf der Geraden 
g:
 
y
=
2x
−
1
 liegen die Punkte 
A
n
 
x
 
|
 
2x
−
1
 die mit B(0|4) die Strecken 
A
n
 
B
 bilden. Für welchen Wert von x ist 
c
=
A
n
 
B
 minimal? Wie lang ist dann 
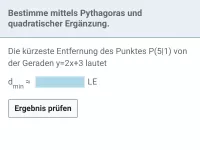
c
min
?
1. Term in Abhängigkeit von x aufstellen:
graphik
c
2
=
x
B
−
x
An
2
+
y
B
−
y
An
2
=
0
−
x
2
+
4
−
2x
−
1
2
=
x
2
+
5
−
2x
2
=
5x
2
−
20x
+
25
2. Quadratische Ergänzung:
c
2
=
5
·
x
2
−
4x
+
25
=
5
·
x
2
−
4x
 
+
2
2
−
2
2
+
25
=
5
·
x
2
−
4x
+
4
−
4
+
25
=
5
·
x
−
2
2
−
4
+
25
=
5
·
x
−
2
2
−
20
+
25
=
5
·
x
−
2
2
+
5
3. Minimalwert und 
x
min
 ablesen:
c
2
min
=
5
 
⇒
 
c
min
=
5
für
 
x
min
=
2
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen