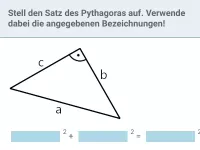
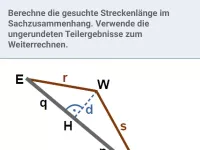
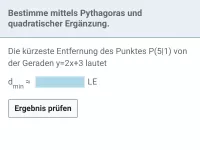
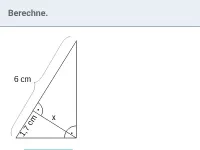
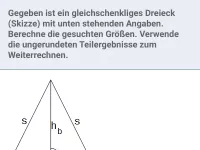
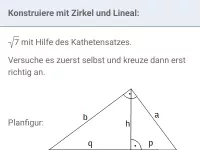
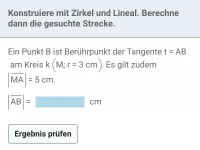
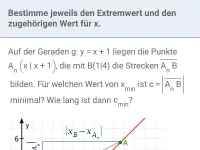
Wie lautet der Satz des Pythagoras ohne Verwendung von Variablen?

Nach dem Satz des Pythagoras gilt in jedem rechtwinkligen Dreieck:

Hypotenuse2 = erste Kathete2 + zweite Kathete2

Zur Erinnerung: Die Hypotenuse ist diejenige der drei Seiten, die dem rechten Winkel gegenüber liegt. Sie ist damit auch immer die längste aller drei Seiten.
Beispiel 1
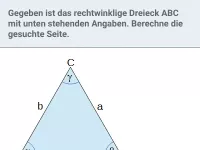
Gegeben ist ein rechtwinkliges Dreieck ABC mit ∠A = 90°; a = 3; b = 2. Bestimme c.
Lösung siehe Video:
Pythagoras, Bestimmung der Hypotenuse, Beispiel
Lernvideo

Pythagoras, Bestimmung der Hypotenuse, Beispiel

Kanal: Mathegym
Beispiel 2
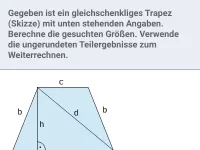
Gegeben ist ein gleichschenkliges Dreieck mit Basis b = 5 LE und Flächeninhalt A = 31 FE. Berechne die Länge seiner Schenkel s.
Lösung siehe Video:
Pythagoras, gleichschenkliges Dreieck, Beispiel
Lernvideo

Pythagoras, gleichschenkliges Dreieck, Beispiel

Kanal: Mathegym
Beispiel 3
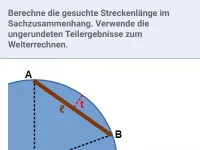
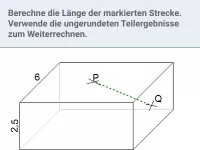
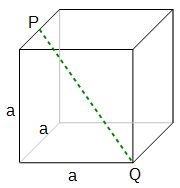
P halbiert die obere Kante. Bestimme 
PQ
 in Abhängigkeit von a.
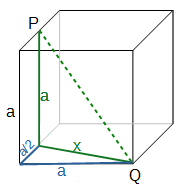
graphik
Lösung:
graphik
Die gesuchte Strecke kann als Hypotenuse eines rechtwinkligen Dreiecks  (grün) mit den Kathetenlängen a und x betrachtet werden. Damit gilt nach Pythagoras:
PQ
2
=
a
2
+
x
2
x wiederum kann als Hypotenuse eines weiteren rechtwinkligen Dreiecks (blau) mit den Kathetenlängen 
0,5a
 und a betrachtet werden, d.h. nach Pythagoras gilt:
x
2
=
a
2
2
+
a
2
=
a
2
4
+
a
2
=
5
4
a
2
Dies eingesetzt in die obere Gleichung führt zu:
PQ
2
=
a
2
+
5
4
 
a
2
=
9
4
 
a
2
 
PQ
=
3
2
a
Pythagoras, Würfel, Beispiel
Lernvideo

Pythagoras, Würfel, Beispiel

Kanal: Mathegym
Beispiel 4
P halbiert die obere Kante. Bestimme 
PQ
 in Abhängigkeit von a.
graphik
Lösung:
graphik
Die gesuchte Strecke kann als Hypotenuse eines rechtwinkligen Dreiecks  (grün) mit den Kathetenlängen a und x betrachtet werden. Damit gilt nach Pythagoras:
PQ
2
=
a
2
+
x
2
x wiederum kann als Hypotenuse eines weiteren rechtwinkligen Dreiecks (blau) mit den Kathetenlängen 
0,5a
 und a betrachtet werden, d.h. nach Pythagoras gilt:
x
2
=
a
2
2
+
a
2
=
a
2
4
+
a
2
=
5
4
a
2
Dies eingesetzt in die obere Gleichung führt zu:
PQ
2
=
a
2
+
5
4
 
a
2
=
9
4
 
a
2
 
PQ
=
3
2
a
!!! Achtung: im Video wird noch die alte Schreibweise 
PQ
 für "Länge der Strecke" verwendet. !!!
Pythagoras, Würfel, Beispiel
Lernvideo

Pythagoras, Würfel, Beispiel

Kanal: Mathegym
Beispiel 5
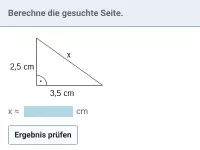
Bestimme x.
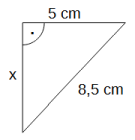
graphik
Es liegt ein rechtwinkliges Dreieck vor. Gegeben ist die Hypotenuse (8,5 cm) und eine Kathete (5 cm). Gesucht ist die Länge der anderen Kathete. Nach dem Satz des Pythagoras gilt:
x
2
+
5
2
=
8,5
2
−
5
2
x
2
=
8,5
2
−
5
2
x
2
=
37,25
x
=
37,25
 
≈
 
6,87 (cm)
Satz des PYTHAGORAS einfach erklärt – rechtwinkliges Dreieck berechnen
Lernvideo

Satz des PYTHAGORAS einfach erklärt – rechtwinkliges Dreieck berechnen

Kanal: MathemaTrick
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen