Was sind die Teiler einer natürlichen Zahl und wie findet man sie?

Jede natürliche Zahl kann durch 1, sich selbst und evtl. weitere Zahlen geteilt werden. Man spricht von Teilern der Zahl. Z.B. hat die Zahl 6 die Teiler 1, 2, 3 und 6.

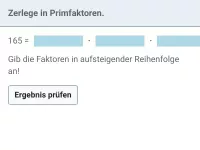
Um alle Teiler einer Zahl zu ermitteln, geht man am besten systematisch vor, z.B. indem man zunächst die Primfaktorzerlegung bestimmt und dann die Primfaktoren systematisch kombiniert.

Beispiel
Bestimme alle Teiler von 360 mit Primfaktorzerlegung.
Lösung:
  • 1. Schritt: Primfaktorzerlegung von 360
360
=
10
·
36
=
2
·
5
·
6
·
6
=
2
·
2
·
2
·
3
·
3
·
5
  • 2. Schritt: alle Teiler von 360 systematisch angeben
Alle Teiler aus EINEM Faktor:
Dies ist immer die 1, sowie alle Primfaktoren, also:
1, 2, 3, 5
Alle Kombinationen aus ZWEI Faktoren:
Am besten gehst du systematisch vor, beginnst mit dem kleinsten Primfaktor und kombinierst ihn mit jedem anderen Primfaktor:
2
·
2
=
4
2
·
3
=
6
2
·
5
=
10
3
·
3
=
9
3
·
5
=
15
Alle Kombinationen aus DREI Faktoren:
Beginne mit drei Zweiern, dann alle Kombis mit zwei Zweiern, dann mit einer und schließlich mit keiner Zwei:
2
·
2
·
2
=
8
2
·
2
·
3
=
12
2
·
2
·
5
=
20
2
·
3
·
3
=
18
2
·
3
·
5
=
30
3
·
3
·
5
=
45
Alle Kombinationen aus VIER Faktoren:
2
·
2
·
2
·
3
=
24
2
·
2
·
2
·
5
=
40
2
·
2
·
3
·
3
=
36
2
·
2
·
3
·
5
=
60
2
·
3
·
3
·
5
=
90
Alle Kombinationen aus FÜNF Faktoren:
2
·
2
·
2
·
3
·
3
=
72
2
·
2
·
2
·
3
·
5
=
120
2
·
2
·
3
·
3
·
5
=
180
Nicht vergessen: das Produkt aus allen Faktoren ist natürlich auch Teiler:
360
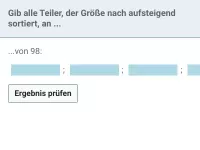
  • 3. Schritt: alle Teiler geordnet aufschreiben
Der Größe nach sortiert lauten die Teiler von 360:
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360
Alle Teiler einer Zahl (mit Primfaktorzerlegung)
Lernvideo

Alle Teiler einer Zahl (mit Primfaktorzerlegung)

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen