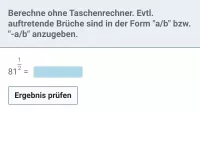
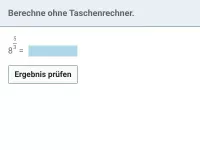
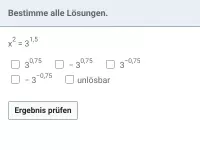
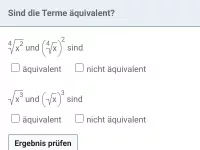
Wie kann man Potenzen mit negativen oder gebrochenen Exponenten in natürliche Exponenten umformen?

Sei r eine positive rationale Zahl. Dann gilt

b−r = 1 / br

Sei b ≥ 0 und n eine natürliche Zahl. Dann gilt

b1/n = n√b

Sei b ≥ 0, m und n natürliche Zahlen. Dann gilt

bm/n = n√(bm) = (n√b)m

Beispiel 1
27
2
3
=
?
 
          
 
0,75
−
2
=
?
Lösung:
27
2
3
=
3
27
2
=
3
2
=
9
0,75
−
2
=
1
0,75
2
=
4
3
2
=
16
9
Beispiel 2
Schreibe jeweils als Potenz (ohne Wurzelzeichen) mit möglichst einfacher Basis:
3
25
9
 
          
 
1
8
Die Regeln oben rückwärts angewandt:
3
25
9
=
3
5
3
2
=
5
3
2
3
- - - - - - - - - - - -
1
8
=
1
2
3
=
1
2
3
2
=
1
2
1,5
=
2
−
1,5
Beispiel 3
Vereinfache jeweils so, dass die Variable nicht im Nenner oder unter der Wurzel steht:
2
3x
2
 
          
 
3
64
27a
Lösung:
2
3x
2
=
2
3
·
1
x
2
=
2
3
 
x
−
2
- - - - - - - - - -
3
64
27a
=
3
64
27
·
1
a
teilweise radizieren
=
4
3
·
3
1
a
=
4
3
·
3
a
−
1
=
4
3
·
a
−
1
3
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen