Wie wandelt man die Darstellungsformen einer quadratischen Funktion ineinander um?
Die Gleichung einer quadratischen Funktion bzw. Parabel kann von jeder Form aus in jede andere Form umgewandelt werden:
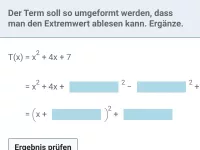
- Allgemeine Form ⇒ Scheitepunktform: mittels quadratischer Ergänzung
- Allgemeine Form ⇒ Nullstellenform: mittels Nullstellenbestimmung, z.B. mit Hilfe der Miternachts- oder der p-q-Formel
- Scheitelpunktform ⇒ allgemeine Form: Ausmultiplizieren (binomische Formel) und vereinfachen
- Scheitelpunktform ⇒ Nullstellenform: mittels Nullstellenbestimmung, wobei hier keine Lösungsformel notwendig ist
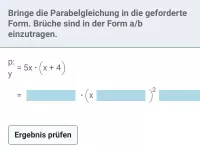
- Nullstellenform ⇒ allgemeine Form: Ausmultiplizieren und vereinfachen
- Nullstellenform ⇒ Scheitelpunktform: xS ergibt sich als Mittelwert der Nullstellen, yS durch Einsetzen von xS in den Funktionsterm
Beispiel
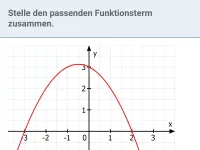
Allgemeine Form - Scheitelpunktform - Nullstellenform: Wandle jeweils von der gegebenen in die beiden anderen Formen um.
a)
y | = |
|
b)
y | = |
|
c)
y | = |
|
Siehe Video

Lernvideo
Umwandlung zw. Scheitelform, Normalform und Nullstellenform
Kanal: Mathegym