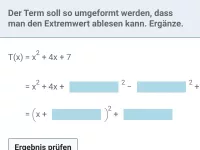
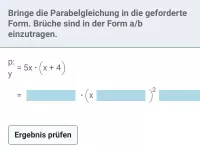
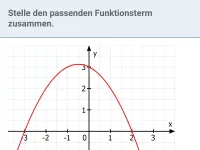
Welche drei Darstellungsformen gibt es für quadratische Funktionen und wie werden sie beschrieben?
Bei der Gleichung einer quadratischen Funktion bzw. Parabel unterscheidet man folgende Formen:
-
Allgemeine Form:
y=ax²+bx+c
Hieraus lässt sich der Schnittpunkt mit der y-Achse (0|c) ablesen.
-
Scheitelpunktform:
y=a·(x−xS)²+yS
Hieraus lässt sich der Scheitelpunkt S(xS|yS) ablesen.
-
Nullstellenform (Produktform/faktorisierte Form):
y=a·(x−x1)·(x−x2)
Hieraus lassen sich die Nullstellen x1 und x2 ablesen.
Beispiel
Stelle, soweit ablesbar, passende Funktionsterme für die Parabeln f und g auf.
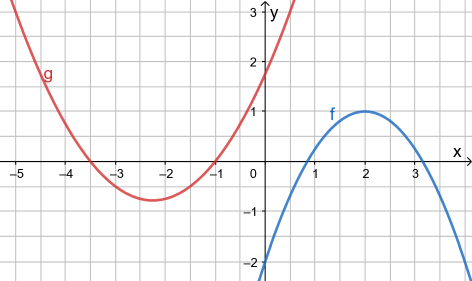
- Parabel g in Nullstellenform
Bei Parabel g können die beiden Schnittstellen
und
mit der x-Achse gut abgelesen werden, daher eignet sich hier die Nullstellen-Form:
| = |
|
| = |
|
y | = |
|
Um den Formfaktor a zu ermitteln, setzt man in die Gleichung einen weiteren Parabelpunkt ein, der gut abgelesen werden kann, z.B.
:
|
| = |
| |||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||
|
- Parabel f in Scheitelpunktform
Bei Parabel f kann der Scheitelpunkt
gut abgelesen werden, daher eignet sich hier die Scheitpunktform:
S |
|
y | = |
|
Auch hier kann man a ermitteln, indem man z.B. den Punkt auf der y-Achse, also
einsetzt:
|
| = |
| |||||||||||||||||||
| = |
|
| ||||||||||||||||||
| = |
| |||||||||||||||||||
| = |
| |||||||||||||||||||
|
- Parabel f in allgemeiner Form
Da bei Parabel f der Schnittpunkt mit der y-Achse
abgelesen werden kann, könnte ihre Gleichung auch in allgemeiner Form wie folgt notiert werden:
|
y | = |
|
Allerdings ist die Scheitelpunktform hier zweckmäßiger, da dann nur noch ein Parameter a bestimmt werden muss und nicht zwei Partameter a und b.