Welche Formen einer Parabelgleichung gibt es und wie wandelt man diese um?
Man unterscheidet bei einer Parabel zwischen
- Allgemeiner Form y = ax² + bx + c ⇒ Ablesen des Schnittpunkts mit der y-Achse (0;c)
- Scheitelpunktform y = a (x - xS)² + yS ⇒ Ablesen des Scheitels S
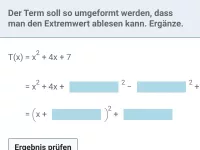
Von der allgemeinen Form ausgehend erhält man die Scheitelpunktform mithilfe der quadratischen Ergänzung.
Beispiel 1
Bringe
in Scheitelpunktform und gib den Scheitel an.
y | = |
|
Lösung siehe Video. Das zweite Video zeigt ähnliche Beispiele.

Lernvideo
Quadratische Funktion, Umwandlung in Scheitelform, Beispiel
Kanal: Mathegym

Lernvideo
QUADRATISCHE ERGÄNZUNG – Parabel in Scheitelpunktform umwandeln, binomische Formel
Kanal: MathemaTrick
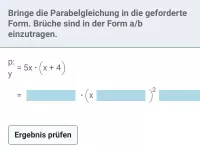
Beispiel 2
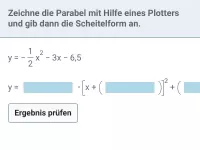
Gegeben ist die Parabel mit der Gleichung
y | = |
|
Die Parabel hat den Scheitel:
S |
|
| = |
| ausklammern | |||||||||||||||||||||||||||||||
| = |
| quadratische Ergänzung | |||||||||||||||||||||||||||||||
| = |
| binomische Formel abtrennen | |||||||||||||||||||||||||||||||
| = |
| Zahlen zusammen rechnen | |||||||||||||||||||||||||||||||
| = |
| ausmultiplizieren | |||||||||||||||||||||||||||||||
| = |
| Scheitel-Koordinaten ablesen | |||||||||||||||||||||||||||||||
|
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈9. Klasse - Aufgaben + Stoff + Video
Quadratische Funktionen - Darstellungsformen
Allgemeine Form (Normalform) - Scheitelpunktform - Nullstenform (Produktform); aus Graph ablesen und Umwandlung, u.a. mit quadratischer Ergänzung -
≈9. Klasse - Aufgaben + Stoff + Video
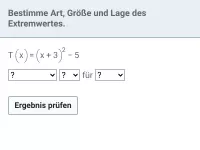
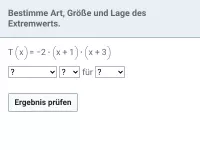
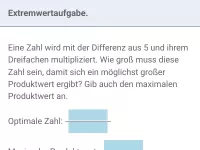
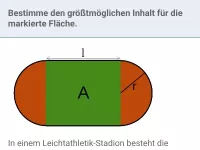
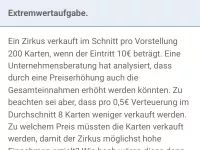
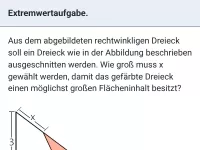
Quadratische Funktionen - Extremwertaufgaben
Minimum und Maximum anhand von Grafiken ablesen können, Extremwertaufgaben/Optimierungsaufgaben im Sachzusammenhang
Ähnliche Themen
- Wie lautet die Gleichung einer Parabel in Scheitelform, wenn die allgemeine Form y = ax² + bx + c und der Scheitel S(s ; t) gegeben sind?
- Wie bestimmt man den Scheitel einer Parabel aus ihren Schnittpunkten mit der x-Achse?
- Wie löst man Extremwertaufgaben in vier Schritten?
- Wie leitet man die allgemeine Form einer Parabelgleichung aus der Scheitelpunktform ab?
- Welche drei Darstellungsformen gibt es für quadratische Funktionen und wie werden sie beschrieben?
- Wie wandelt man die Darstellungsformen einer quadratischen Funktion ineinander um?
- Wie bestimmt man das Maximum bzw. Minimum einer Parabelfunktion und wann tritt es auf?