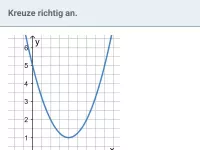
Wie bestimmt man den Scheitel einer Parabel aus ihren Schnittpunkten mit der x-Achse?

Weiß man, dass eine Parabel die x-Achse an den Stellen x1 und x2 schneidet, so kann man ihren Scheitel S leicht bestimmen:
  • xS = (x1 + x2) : 2
    Begründung: xS (also die x-Koordinate des Scheitels) liegt aus Symmetriegründen genau in der Mitte des Intervalls [x1 ; x2]
  • yS = p(xS)
    d.h. die y-Koordinate erhält man durch Einsetzen von xS in den Funktionsterm der Parabel
Beispiel 1
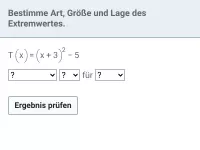
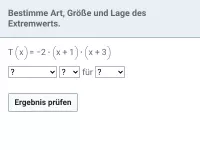
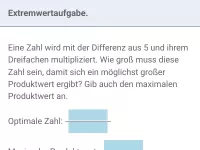
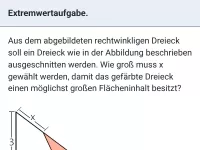
Bestimme Art, Größe und Lage des Extremwerts.
T
 
x
=
1
2
·
2x
+
1
·
x
−
2,5
Da der quadratische Term in Nullstellenform gegeben ist, kann man die Nullstellen 
x
1
=
−
0,5
 und 
x
2
=
2,5
 sofort ablesen. Die zugehörige Parabel besitzt ihren Scheitel genau in der Mitte, also bei 
x
S
=
−
0,5
+
2,5
:
2
=
1
. Der zugehörige y-Wert ist 
y
S
=
T
 
1
=
1
2
·
3
·
−
1,5
=
−
2,25
. Da es sich um eine nach oben geöffnete Parabel handelt (ausmultipliziert 
T
 
x
=
x
2
+
…
), liegt bei 
x
=
1
 also das 
Minimum
−
2,25
 vor.
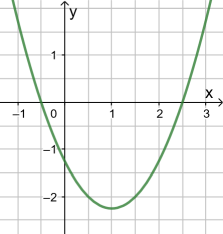
graphik
Beispiel 2
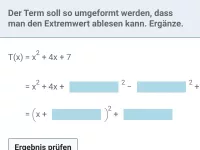
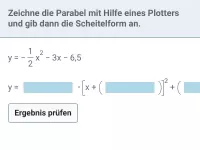
Die Parabel mit der Gleichung 
y
=
−
3x
2
−
2x
+
1
 schneidet die x-Achse an den Stellen 
x
1
=
−
1
 und 
x
2
=
1
3
. Bestimme die Koordinaten des Scheitelpunkts.
Der Scheitelpunkt liegt genau in der Mitte zwischen den beiden Nullstellen:
x
S
=
−
1
+
1
3
:
2
=
−
1
3
Der y-Wert ergibt sich durch Einsetzen von 
x
S
=
−
1
3
 in den Funktionsterm:
y
S
=
−
3
·
−
1
3
2
−
2
·
−
1
3
+
1
=
−
1
3
+
2
3
+
1
=
4
3
graphik
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen