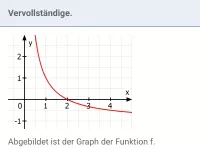
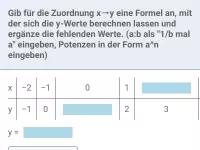
Was ist eine Funktion und wie kann man feststellen, ob eine Zuordnung eine Funktion ist?
Eine Funktion ist eine EINDEUTIGE Zuordnung.
Jedem Ausgangswert x kann genau ein Funktionswert y zugeordnet werden.
Natürlich können mehrere Ausgangswerte zum selben Funktionswert führen, aber nicht umgekehrt!
Um zu zeigen, dass eine Zuordnung KEINE Funktion ist, reicht es, einen einzigen Ausgangswert zu finden, dem mehrere Funktionswerte zugeordnet sind.
Beispiel
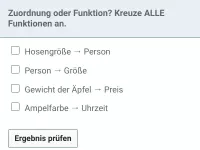
Gib an, ob es sich bei folgenden Zuordnungen um Funktionen handelt und begründe:
1) Auto → Fahrzeughalter
2) Fahrzeughalter → Auto
3) x → y = f(x)
4) x → y = g(x)

Lösung:
Bei 1) handelt es sich um eine Funktion, da jedem Auto genau ein Fahrzeughalter zugeordnet werden kann.
Bei 2) liegt keine Funktion vor, da ein Fahrzeughalter mehrere Autos besitzen kann.
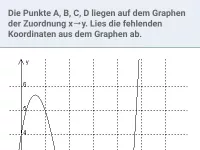
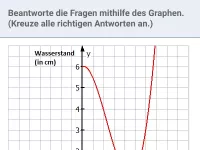
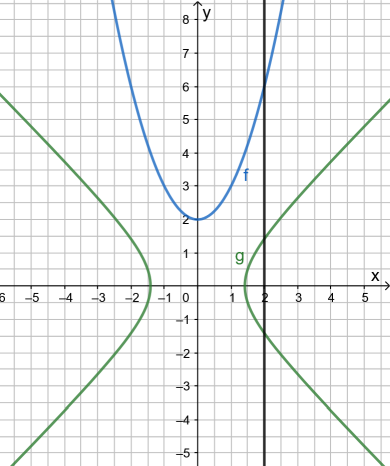
Bei 3) liegt eine Funktion vor, da jedem x genau ein
zugeordnet werden kann. Anders ausgedrückt: jede senkrechte Gerade schneidet den blauen Graphen genau einmal.
y | = | f(x) |
Bei 4) liegt keine Funktion vor, da z.B. dem Wert
zwei unterschiedliche y-Werte zugeordnet werden können (zwei Schnittpunkte der senkrechten Geraden mit dem grünen Graphen).
x | = | 2 |

Lernvideo
Was ist eine Funktion? - Einfach erklärt
Kanal: Mathe - simpleclub
Siehe auch