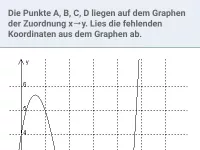
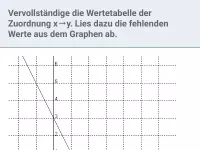
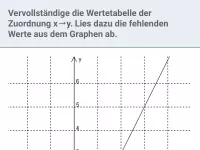
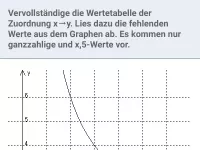
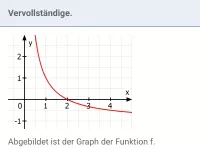
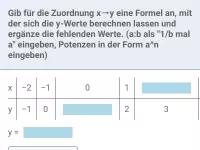
Wie hängen die Gleichung und der Graph einer Funktion zusammen?
Gegeben ist eine Funktion f mit der Funktiongleichung \(y=f(x)\) und dem Graphen \(G_f.\) Dann gilt:
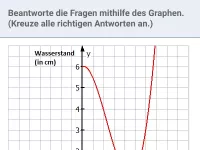
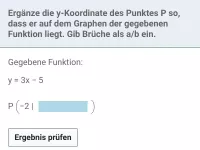
- Liegt ein Punkt P(x|y) auf dem Graphen, so erfüllen seine Koordinaten x und y die Funktionsgleichung.
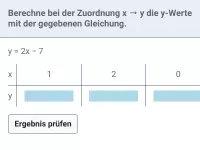
- Erfüllen zwei Werte x und y die Funktionsgleichung (und gehört x zur Definitionsmenge von f), so liegt der entsprechende Punkt auf dem Graphen.
Beispiel
Ergänze:
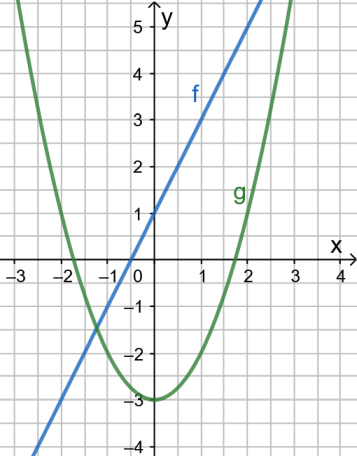
- Da der Punkt \(P(1|\colorbox{yellow}{$?$})\) auf \(G_f\) liegt, gilt die Gleichung \(f(\colorbox{yellow}{$?$})=\colorbox{yellow}{$?$}.\)
- Da der Punkt \(P(\colorbox{yellow}{$?$}|-4)\) auf \(G_g\) liegt, gilt die Gleichung \(g(\colorbox{yellow}{$?$})=\colorbox{yellow}{$?$}.\)
- Da der Punkt \(P(1|\colorbox{yellow}{$3$})\) auf \(G_f\) liegt, gilt die Gleichung \(f(\colorbox{yellow}{$1$})=\colorbox{yellow}{$3$}.\)
- Da der Punkt \(Q(\colorbox{yellow}{$-2,5$}|-4)\) auf \(G_g\) liegt, gilt die Gleichung \(g(\colorbox{yellow}{$-2,5$})=\colorbox{yellow}{$-4$}.\)
Siehe auch
