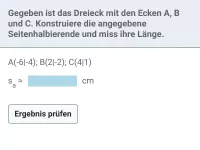
Wie konstruiert man den Umkreis eines Dreiecks?
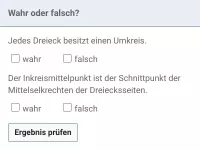
Die Punkte der Winkelhalbierenden besitzen die Eigenschaft, dass sie zu beiden Schenkeln denselben Abstand haben. Daher gilt folgender Satz:
Die drei Winkelhalbierenden eines jeden Dreiecks schneiden sich in einem Punkt. Dieser Punkt hat von allen drei Seiten denselben Abstand, ist also der Mittelpunkt des Inkreises.
Beispiel
Gegeben ist das folgende Dreieck. Konstruiere den Inkreis.
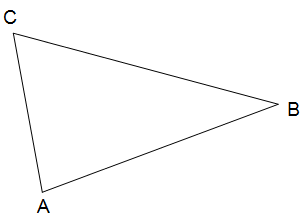
Lösung: Konstruiere zunächst eine Winkelhalbierende.
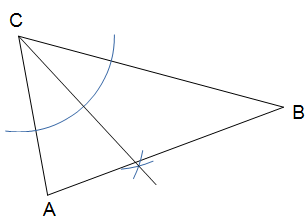
Dann eine zweite. Beide schneiden sich im Mittelpunkt M des Inkreises.
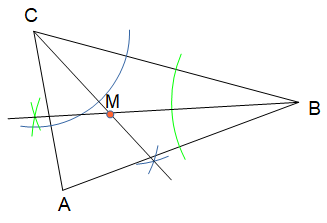
Fälle das Lot von M auf eine der Dreieckseiten, um einen Kreispunkt P zu ermitteln.
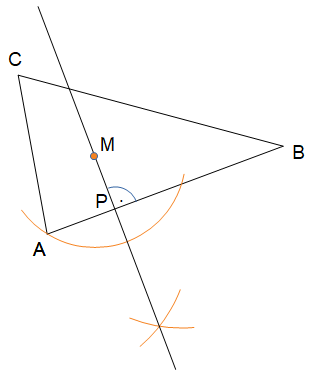
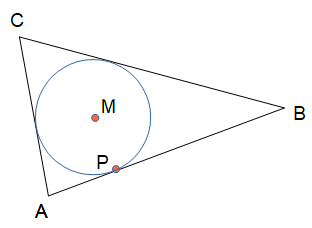
Jetzt kann der Inkreis um M durch P gezogen werden.
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈7. Klasse - Aufgaben + Stoff
Dreiecke - Inkreis und Umkreis
Mittelsenkrechte, Winkelhalbierende, Umkreis, Inkreis; Konstruktionsaufgaben -
≈7. Klasse - Aufgaben + Stoff
Konstruktion mit Zirkel und Lineal - Standardkonstruktionen
Mittelsenkrechte, Winkelhalbierende, Lot, Höhe, Inkreis, Umkreis, Höhenschnittpunkt, Thaleskreis