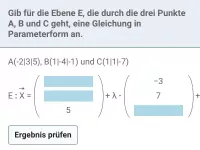
In welchen besonderen Fällen legen zwei Geraden, die in Parameterform gegeben sind, eine Ebene fest und wie erhält man jeweils die Parameterform dieser Ebene?
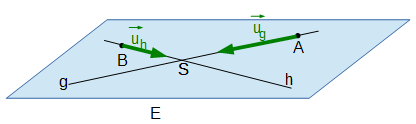
Zwei Geraden g und h legen eine Ebene fest, wenn sie
- sich in einem Punkt schneiden:
- echt parallel sind (d.h. parallel und nicht identisch):
Beispiel
| = |
|
Die Ebene E enthält die Geraden g und h, die Ebene F die Geraden g und i. Gib für E und F jeweils eine Gleichung in Parameterform an.
Lösung:
- Ebene E
|
 |
|
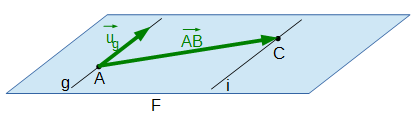
- Ebene F
| = |
|
Als Aufpunkt kann A (möglich wäre auch C) verwendet werden, also:
|
 |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie erhält man die Ebene E durch drei gegebene Punkte A, B und C in Parameterform?
- Gegeben ist eine Ebene E in Parameterform und ein Punkt P. Wie prüft man, ob P∈E?
- Welche besondere Lagebeziehungen zwischen einer Ebene und dem KOSY sind möglich und welche Rolle spielen dabei der Stützvektor ("Aufpunkt") und die beiden Richtungsvektoren?
- Wie können eine Gerade und eine Ebene im Raum zueinander liegen und wie ermittelt man die genaue Lage rechnerisch?