Wie berechnet man für eine Bernoulli-Kette der Länge n die Wahrscheinlichkeit P(X=r) ?

Bernoulli Formel:

Für eine Bernoulli-Kette der Länge n lässt sich die Wahrscheinlichkeit P(X=r), dass die Zufallsgröße X genau r Treffer (Trefferwahrscheinlichkeit p) hat mit der Bernoulli-Formel berechnen:

Bn,p = P(X=r) = (nr) · pr · (1 − p)n-r
Beispiel 1
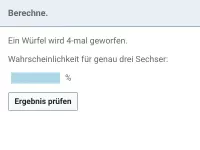
Ein Würfel wird 5 Mal geworfen.
Wahrscheinlichkeit für genau vier Einser:
 
?%
Wahrscheinlichkeit für höchstens zwei Quadratzahlen:
 
?%
  • Wahrscheinlichkeit für genau vier Einser:
Hier handelt es sich um eine Bernoulli-Kette der Länge n = 5 (5mal würfeln). Die Zufallsgröße X beschreibt die Anzahl der gewürfelten 1er und hat die Trefferwahrscheinlichkeit p=1/6.
B
5,
 
1
6
 
4
=
P
 
X
=
4
=
5
4
·
1
6
4
·
5
6
5
−
4
=
5
·
4
·
3
·
2
1
·
2
·
3
·
4
·
1
6
4
·
5
6
1
=
5
1
·
1
1296
·
5
6
=
25
7776
 
≈
 
0,0032
 
≈
 
0,3
 
%
  • Wahrscheinlichkeit für höchstens zweimal Quadratzahl
Hier handelt es sich um eine Bernoulli-Kette der Länge n = 5 (5-mal würfeln). Die Zufallsgröße X beschreibt die Anzahl der gewürfelten Quadratzahlen (1 und 4) und hat die Trefferwahrscheinlichkeit p=1/3. "Höchstens zweimal Quadratzahl" bedeutet keine, eine oder zwei Quadratzahlen.
P(X≤2)
=
P(X=0)
+
P(X=1)
+
P(X=2)
=
5
0
·
1
3
0
·
2
3
5
P(X=0)
+
5
1
·
1
3
1
·
2
3
4
P(X=1)
+
5
2
·
1
3
2
·
2
3
3
P(X=2)
=
1
·
32
243
+
5
1
·
1
3
·
16
81
+
5
·
4
1
·
2
·
1
9
·
8
27
=
32
243
+
80
243
+
80
243
=
192
243
=
64
81
≈
 
0,790
=
79,0
 
%
Beispiel 2
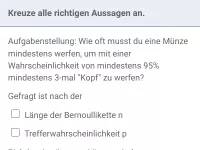
Wie oft muss ein Würfel mindestens geworfen werden, um mit einer Wahrscheinlichkeit von mindestens 80% mindestens eine 1 zu würfeln?
Hier handelt es sich um eine Bernoulli-Kette unbekannter Länge n. Die Trefferwahrscheinlichkeit ("Eins würfeln") beträgt 1/6. Damit ergibt sich:
 
P
 
X ≥ 1
≥
0,8
Gegenereignis
P
 
X=0
≤
0,2
Erläuterung zu den beiden letzten Zeilen: Das Gegenereignis von "X ≥ 1" (mindestens eins) ist "X=0" (keins). Ereignis und Gegenereignis ergänzen sich bzgl. ihrer Wahrscheinlichkeit zu 1. Wenn das eine also größer oder gleich 0,8 ist, muss das andere logischer Weise kleiner oder gleich 0,2 sein.
B
n,
 
1
6
 
0
≤
0,2
5
6
n
≤
0,2
Erläuterung: die Potenz in der Zeile oben ergibt sich durch Einsetzen von 0 in die Bernoulli-Formel + Vereinfachung.
5
6
n
≤
0,2
log
n
·
log
 
5
6
≤
log 0,2
:
log
 
5
6
n
≥
log 0,2
log
 
5
6
Erläuterung: Das Ungleichheitszeichen hat sich in der letzten Zeile umgedreht, da durch einen negativen Wert geteilt wurde.
n ≥8,8...
Da es nur "ganze" Würfe gibt muss also mindestens 9 mal geworfen werden.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen