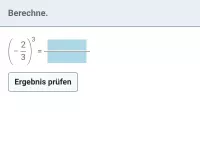
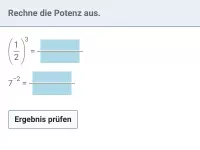
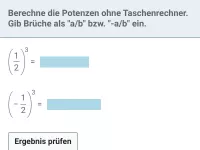
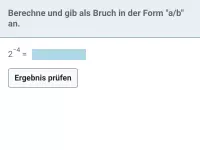
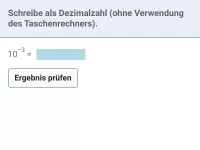
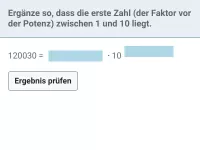
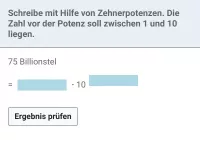
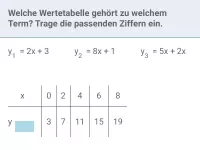
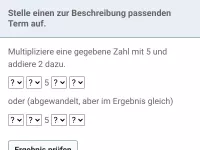
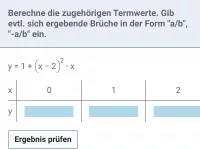
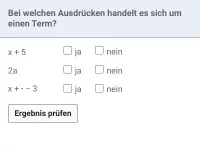
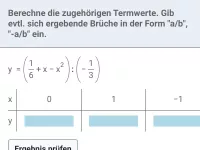
Was bedeutet eine Potenz mit negativer Hochzahl, z.B. \(2^{-3}\)?
Ein negativer Exponent bedeutet, dass man den Kehrwert der Potenz mit positivem Exponenten bildet:
\[
a^{-n} = \frac{1}{a^{n}}
\qquad (a \ne 0)
\]
Der Exponent wird dabei positiv:
\[
a^{-1} = \frac{1}{a}, \quad
a^{-2} = \frac{1}{a^2}, \quad
a^{-3} = \frac{1}{a^3}, \dots
\]
Einfaches Zahlenbeispiel:
\[ 4^{-2} = \frac{1}{4^2} = \frac{1}{16} \]Beispiel
Bestimme das Ergebnis.
\(\displaystyle \left(\frac35\right)^{-3}\)
\(\displaystyle \left(\frac35\right)^{-3}=\left(\frac53\right)^{3}=\frac53\cdot\frac53\cdot\frac53=\frac{125}{27}\)
oder:
\(\displaystyle \left(\frac35\right)^{-3}=\frac1{\left(\frac35\right)^{3}}=\frac{1} {\left(\frac53\right)\cdot\left(\frac53\right)\cdot\left(\frac53\right)}=\frac{1}{\frac{27}{125}}=\frac{125}{27}\)Genauer:
\(\displaystyle \frac{1}{\frac{27}{125}}=1:\frac{27}{125}=1 \cdot \frac{125}{27}=\frac{125}{27}\)Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
-
≈6. Klasse - Aufgaben + Stoff
Brüche - Potenzen
Potenz von Brüchen und gemischten Zahlen, Potenzwerte mit negativen ganzzahligen Exponenten -
≈8. Klasse - Aufgaben + Stoff
Potenzen mit negativen ganzzahligen Exponenten
Potenzen mit negativer Hochzahl richtig interpretieren und berechnen -
≈7. Klasse - Aufgaben + Stoff + Video
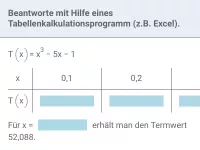
Terme - Berechnung von Termwerten
Berechnung von Termwerten bei Termen mit maximal 2 Variablen