Wie berechnet man mehrere aufeinanderfolgende prozentuale Veränderungen?

Ergeben sich mehrere prozentuale Veränderungen hintereinander, so lässt sich ähnlich wie bei der Grundgleichung der Prozentrechnung eine Gleichung formulieren, in der aber mehrere Prozentsätze vorkommen.
Beispiel
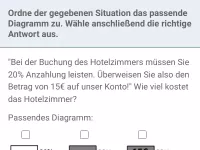
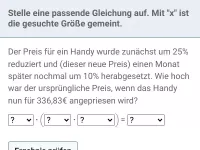
Von 2002 bis 2005 ist der Immobilienpreis in München um 10% zurückgegangen. Von 2005 bis 2014 ist er um 70% gestiegen. Wieviel Euro zahlte man 2002 pro Quadratmeter, wenn der Preis 2014 bei 6€/m² lag? Um wieviel Prozent ist Preis insgesamt gestiegen im Zeitraum 2002 bis 2014?
Lösung:
100%
−
10%
=
90%
=
0,9
100%
+
70%
=
170%
=
1,7
1,7
·
0,9
·
x
=
6
 
€/
m
2
ausmultiplizieren
1,53
·
x
=
6
 
€/
m
2
:
1,53
x
=
6
 
€/
m
2
:
1,53
 
≈
 
3,92
 
€/
m
2
Der ursprüngliche Quadratpreis betrug also ungefähr 3€ 92ct. Der Gesamtanstieg wird durch den oben ausgerechneten Gesamtfaktor 
1,53
=
153%
 ausgedrückt. D.h. der Gesamtanstieg beträgt 53%.

Ausführlicher: siehe Video
Größe verändert sich zweimal prozentual - Grundwert gesucht
Lernvideo

Größe verändert sich zweimal prozentual - Grundwert gesucht

Kanal: Mathegym
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen