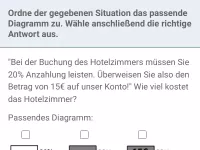
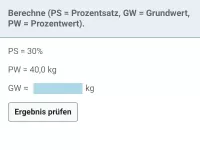
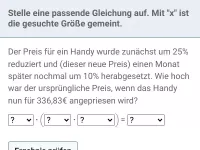
Wie hilft ein Streifendiagramm, Fehler in der Prozentrechnung zu vermeiden?

Vermeide beim Prozentrechnen die folgenden Fehler:
  • Falsche Zuordnung des Grundwerts
  • Prozentwert und Prozentsatz gehören nicht zusammen
Ein gutes Mittel, um solche Fehler zu vermeiden, ist die Veranschaulichung einer Situation in einem Streifendiagramm: Es besteht aus einem unterteilten Rechteck, bei dem im Inneren die gegebenen Größen und am Rand die passenden Prozentsätze notiert werden (siehe folgendes Beispiel).
Beispiel
Veranschauliche die folgende Aufgabe durch ein Diagramm und löse sie:
In Bayern gibt es heute auf 2,45 Millionen Hektar Waldgebiete. Vor der Römerzeit war Bayern auf seiner 
70
 
000km
2
 großen Fläche noch so gut wie vollständig bewaldet. Welcher prozentuale Anteil der Waldfläche wurde also innerhalb der letzten 2000 Jahre gerodet?
Passendes Diagramm:
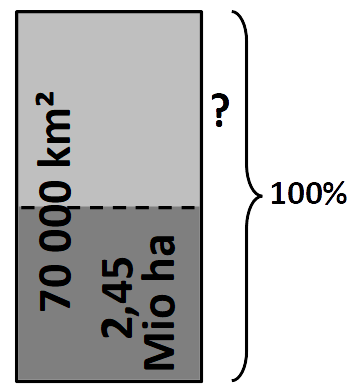
graphik
Anhand des Diagramms kann man leichter entscheiden, welche Größe der Grundwert ist. Außerdem gelingt es einem besser, einem gegebenen Prozentwert den passenden Prozentsatz zuzuordnen (und umgekehrt).
Anhand des Diagramms erkennt man:
  • Der Grundwert ist die Waldfläche vor der Römerzeit, also 
    GW
    =
    70
     
    000km
    2
    .
  • Zum gesuchten Prozentsatz gehört die Differenz der Waldflächen als Prozentwert:
PW
=
70
 
000km
2
−
2
 
450
 
000ha
=
70
 
000km
2
−
24
 
500km
2
=
45
 
500km
2
PS
=
PW
GW
=
45500km
2
70000km
2
       
=
455
700
=
65
100
=
65%
Antwort: Es wurden 65% der Waldfläche in Bayern gerodet.
Siehe auch

Mathe-Aufgaben zu diesem Thema

Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.

Ähnliche Themen