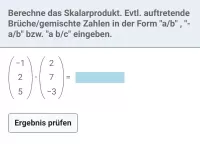
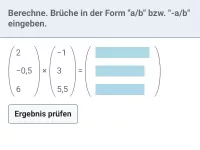
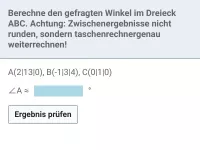
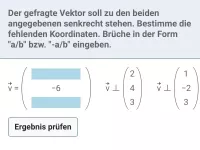
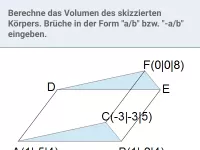
Wie berechnet man das Skalarprodukt zweier Vektoren und welche Art von Ergebnis liefert es?
Das Skalarprodukt zweier Vektoren ist eine reelle Zahl (kein Vektor!).
Definiert wird es als Produkt ihrer Längen, multipliziert mit cos(α), wobei mit α der Winkel zwischen beiden Vektoren gemeint ist (stelle sie dir in ihren Fußpunkten zusammengelegt vor, 0° ≤ α ≤ 180°).
Noch einfacher lässt es sich berechnen, indem man die Koordinaten beider Vektoren zeilenweise multipliziert und die Produkte addiert.
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
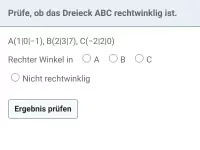
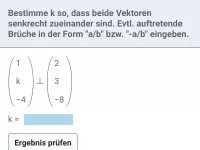
- Wie kann man feststellen, ob zwei Vektoren senkrecht zueinander sind?
- Wie berechnet man den Winkel zwischen zwei Vektoren?
- Wie berechnet man die Koordinaten des Produktvektors beim Vektorprodukt zweier Vektoren?
- Welche Eigenschaft hat das Vektorprodukt zweier Vektoren bezüglich des aufgespannten Parallelogramms?
- Wie ist die Lage des Vektorprodukts zweier Vektoren relativ zu diesen?
- Was ist ein Spat und wie wird sein Volumen berechnet?
- Wie berechnet man das Volumen einer Pyramide, die von drei Vektoren aufgespannt wird?