Wie berechnet man den Winkel zwischen zwei Vektoren?
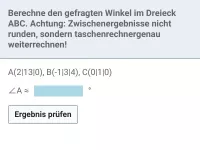
Für den Winkel α zwischen zwei Vektoren (stelle sie dir in ihren Fußpunkten zusammengelegt vor, 0° ≤ α ≤ 180°) gilt:
cos(α) = Skalarprodukt beider Vektoren : Produkt ihrer Längen
Beispiel
| = |
|
| = |
|
φ | = |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie berechnet man das Skalarprodukt zweier Vektoren und welche Art von Ergebnis liefert es?
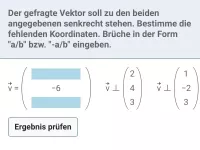
- Wie kann man feststellen, ob zwei Vektoren senkrecht zueinander sind?
- Wie berechnet man die Koordinaten des Produktvektors beim Vektorprodukt zweier Vektoren?
- Welche Eigenschaft hat das Vektorprodukt zweier Vektoren bezüglich des aufgespannten Parallelogramms?
- Wie ist die Lage des Vektorprodukts zweier Vektoren relativ zu diesen?
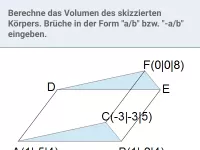
- Was ist ein Spat und wie wird sein Volumen berechnet?
- Wie berechnet man das Volumen einer Pyramide, die von drei Vektoren aufgespannt wird?