Wie kann man feststellen, ob zwei Vektoren senkrecht zueinander sind?
Zwei Vektoren (jeweils ungleich dem Nullvektor) stehen genau dann senkrecht zueinander, wenn ihr Skalarprodukt null ist.
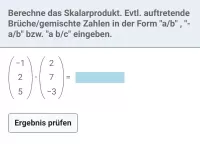
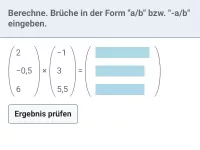
Beispiel 1
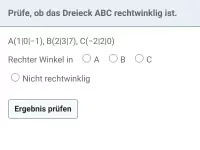
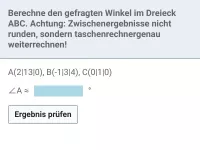
Gegeben ist das Dreieck mit den Eckpunkten A(0|9|-1), B(-2|-5|3) und C(-2|-3|1). Prüfe, ob es sich um ein rechtwinkliges Dreieck handelt.
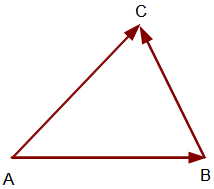
Lösung: Betrachte die drei Seiten des Dreiecks als Vektoren. Wenn zwei dieser Vektoren senkrecht zueinander stehen, handelt es sich um ein rechtwinkliges Dreieck.
| = |
|
| = | 180 |
| = |
|
| = |
|
In keinem Fall ergibt sich der Wert Null, also handelt es sich um kein rechtwinkliges Dreieck.
Beispiel 2
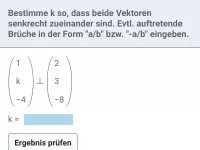
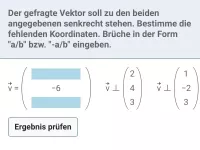
Bestimme k so, dass beide Vektoren senkrecht zueinander sind.
\[ \begin{pmatrix} 2 \\ k \\ 5 \end{pmatrix} \perp \begin{pmatrix} 3 \\ 4 \\ -6 \end{pmatrix} \]Lösung:
Damit beide Vektoren senkrecht zueinander sind, muss das Skalarprodukt 0 sein:
\[ \begin{pmatrix} 2 \\ k \\ 5 \end{pmatrix} \circ \begin{pmatrix} 3 \\ 4 \\ -6 \end{pmatrix} = 6 + 4k - 30 \] \[ \begin{align*} 6 + 4k - 30 &= 0 \\ -24 + 4k &= 0 &|& \quad +24 \\ 4k &= 24 &|& \quad \div 4 \\ k &= 6 \end{align*} \]Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie berechnet man das Skalarprodukt zweier Vektoren und welche Art von Ergebnis liefert es?
- Wie berechnet man den Winkel zwischen zwei Vektoren?
- Wie berechnet man die Koordinaten des Produktvektors beim Vektorprodukt zweier Vektoren?
- Welche Eigenschaft hat das Vektorprodukt zweier Vektoren bezüglich des aufgespannten Parallelogramms?
- Wie ist die Lage des Vektorprodukts zweier Vektoren relativ zu diesen?
- Was ist ein Spat und wie wird sein Volumen berechnet?
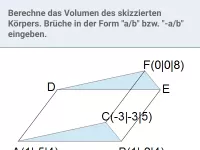
- Wie berechnet man das Volumen einer Pyramide, die von drei Vektoren aufgespannt wird?