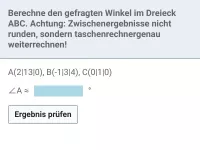
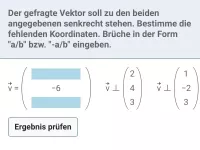
Was ist ein Spat und wie wird sein Volumen berechnet?
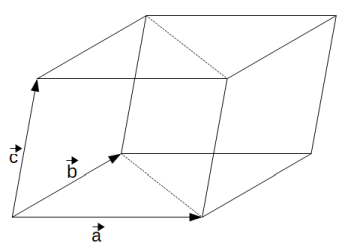
Ein Spat ("schräge Schuhschachtel") wird von drei Vektoren aufgespannt. Um sein Volumen zu berechnen, gehe wie folgt vor:
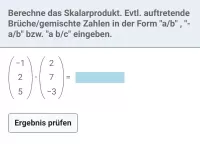
- Nimm zwei (von den drei aufspannenden Vektoren) und berechne deren Vektorprodukt.
- Berechne dann das Skalarprodukt aus dem Ergebnis von (1) und dem dritten Vektor.
- Der Betrag davon ist das Spatvolumen.
Beispiel
Berechne das Volumen des von den Vektoren
,
und
aufgespannten Prismas mit
,
und
.
a
b
c
a
| = |
|
b
| = |
|
c
| = |
|
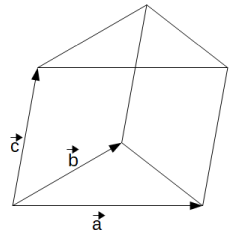
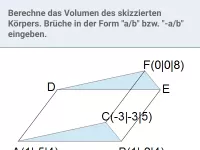
Lösung: Das Prisma passt genau zweimal in den Spat, der von denselben Vektoren aufgespannt wird. Berechne also dessen Volumen und teile das Ergebnis durch 2.
| = |
| |||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||
|
| = |
| |||||||||||||||||||||||||||||||||||||||||||
| = |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie berechnet man das Skalarprodukt zweier Vektoren und welche Art von Ergebnis liefert es?
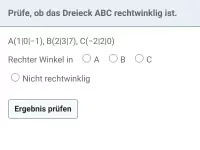
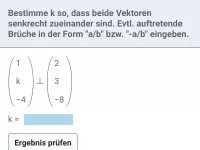
- Wie kann man feststellen, ob zwei Vektoren senkrecht zueinander sind?
- Wie berechnet man den Winkel zwischen zwei Vektoren?
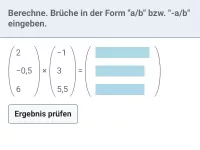
- Wie berechnet man die Koordinaten des Produktvektors beim Vektorprodukt zweier Vektoren?
- Welche Eigenschaft hat das Vektorprodukt zweier Vektoren bezüglich des aufgespannten Parallelogramms?
- Wie ist die Lage des Vektorprodukts zweier Vektoren relativ zu diesen?
- Wie berechnet man das Volumen einer Pyramide, die von drei Vektoren aufgespannt wird?