Wie berechnet man die Schnittpunkte einer Geraden mit den Koordinatenachsen?
Schnittpunkte mit den Koordinatenachsen:
Jede Gerade, die nicht parallel zu einer der Koordinatenachsen verläuft, schneidet jede Achse genau einmal.- Der Schnittpunkt mit der y-Achse ist dort, wo die x-Koordinate den Wert 0 annimmt. Er kann aus der Geradengleichung abgelesen werden, z.B ist bei y=2x−3 der y-Achsenabschnitt −3 und damit Sy(0|−3)
- Am Schnittpunkt mit der x-Achse ist die y-Koordinate 0. Um die x-Koordinate des Schnittpunkts zu bestimmen, setzt du in der Geradengleichung y=0 und löst die Gleichung nach x auf.
- Die Stelle x, an der die Gerade die x-Achse schneidet, bezeichnet man auch als Nullstelle.
Beispiel
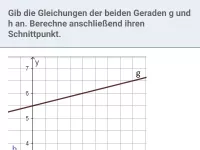
Bestimme die Schnittpunkte der Gerade
mit den Koordinatenachsen.
g: y | = |
|
Die Schnittpunkte sehen immer folgendermaßen aus:
Schnittpunkt mit der y-Achse
(0|?)
S | y |
Schnittpunkt mit der x-Achse
(?|0)
S | x |
-----------------------------------
Der Schnittpunkt mit der y-Achse kann direkt aus der Geradengleichung abgelesen werden.
S | y |
Formal setzt du die x-Koordiante 0 ein, damit ergibt sich
| = |
|
-----------------------------------
Für den Schnittpunkt mit der x-Achse setzt du als y-Koordinate 0 ein und löst die Gleichung:
| = |
|
| ||||||||||
| = |
|
| ||||||||||
| = |
| |||||||||||
Der Schnittpunkt mit der x-Achse ist
(
|0)
S | x |
− |
|
Siehe auch