Welche Summanden bestimmen das Verhalten einer ganzrationalen Funktion nahe der y-Achse?
Bei einer ganzrationalen Funktion entscheiden die Summanden mit den niedrigsten x-Potenzen, wie sich die Funktion in der Nähe der y-Achse verhält.
Beispiel
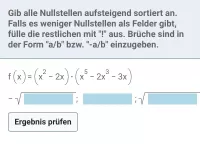
Wie verhalten sich die Funktionsgraphen in der Umgebung der y-Achse?
| = |
|
| = |
|
Lösung:
| = |
|
In unmittelbarer Umgebung der y-Achse verhält sich der Graph wie die Gerade
und zwar umso deutlicher, je näher man bei der y-Achse bleibt:
y | = |
|

| = |
|
In unmittelbarer Umgebung der y-Achse verhält sich der Graph wie die Parabel
y | = |
|

Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie funktioniert Polynomdivision und welchen Grad hat das Ergebnispolynom?
- Was ist der Vorteil eines faktorisierten Funktionsterms?
- Wie funktioniert die Substitutionsmethode in der Mathematik?
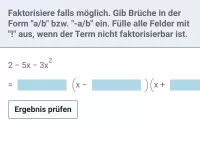
- Wie kann ein quadratischer Term faktorisiert werden und welche Rolle spielen dabei die Lösungen der Nullgleichung?
- Wie kann man Polynome vom Grad 3 oder höher faktorisieren?
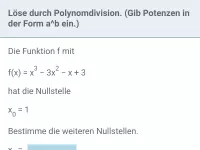
- Wie kann die Polynomdivision zur Bestimmung der Nullstellen einer ganzrationalen Funktion 3. Grades oder höher eingesetzt werden?