Was versteht man unter Fehlern erster und zweiter Art in der Statistik?
- Fehler erster Art (α´): Die Nullhypothese wird abgelehnt (Z ∈ A), obwohl sie richtig ist
- Fehler zweiter Art (β): Die Nullhypothese wird nicht abgelehnt (Z ∈ A), obwohl sie falsch ist
Die zugehörigen Wahrscheinlichkeiten nennt man Risiko erster bzw. zweiter Art.
Beispiel
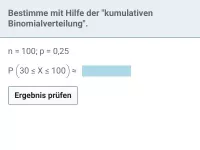
Bestimme die Fehler erster und zweiter Art (letzteren für p = 0,05):
n = 30
| = | {2; 3;...; 30} |
| = | {0; 1} |
- Fehler erster Art
Der Fehler erster Art geht davon aus, dass die Nullhypothese zutrifft, daher kann p = 0,1 als Trefferwahrscheinlichkeit verwendet werden. Dass sie (trotzdem) abgeleht wird heißt, dass
Z ∈ |
|
| = |
= |
|
- Fehler zweiter Art
Die Wahrscheinlichkeit für den Fehler zweiter Art kann nicht ohne weitere Annahmen bestimmt werden. Was man braucht, ist ein Wert für p. Hier soll p = 0,05 (< 0,1) angenommen werden. Man geht also davon aus, dass die Nullhypothese nicht zutrifft. Dass sie trotzdem nicht abgelehnt wird heißt, dass
Z ∈ A:
| = |
| = |
= |
|
Siehe auch
Mathe-Aufgaben zu diesem Thema
Online-Übungen, die du direkt im Browser bearbeiten und lösen kannst! Mit ausführlichen Musterlösungen, professionellen Erklär-Videos und gezielten Hilfestellungen.
Ähnliche Themen
- Wie formuliert man Null- und Gegenhypothese sowie kritischen und unkritischen Bereich?
- Wie bestimmt man Wahrscheinlichkeiten der Form P(Z≤k) und P(Z>k)?
- Was versteht man unter Fehlern erster und zweiter Art in der Statistik?
- Wie beeinflusst der Annahmebereich der Nullhypothese das Risiko erster Art?
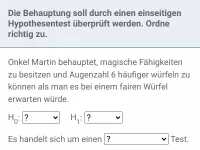
- Was versteht man unter einem einseitigen Signifikanztest?
- Was sind Nullhypothese, Gegenhypothese, Testgröße, kritischer und nichtkritischer Bereich sowie rechtsseitiger und linksseitiger Test bei einem einseitigen Hypothesentest?