Wie bestimmt man Wahrscheinlichkeiten der Form P(Z≤k) und P(Z>k)?

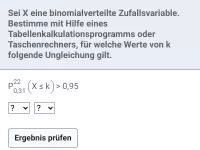
Wahrscheinlichkeiten der Art P( X ≤ k ) einer binomial verteilten Zufallsgröße X können mit unterschiedlichen Hilfsmitteln (WTR, CAS/MMS, GTR, Tafelwerk) bestimmt werden. Man beachte, welche Hilfsmittel für die Prüfung zugelassen sind!

Um P( Z > k ) zu bestimmen, ermittelt man erst den Wahrscheinlichkeitswert für das Gegenereignis "Z ≤ k" und zieht diesen dann von 1 ab.

Beispiel 1

200

0,3

Z ≥ 60

Lösung: Das Gegenereignis von "Z ≥ 60" lautet "Z < 60", also "Z ≤ 59" (Ableseform). Der Tabelle entnimmt man:

200

0,3

Z ≤ 59

≈

0,47335

und somit

200

0,3

Z ≥ 60

≈

−

0,47335

0,52665

Beispiel 2

Eine Urne enthält eine weiße und 7 schwarze Kugeln. Wie oft musst du mindestens eine Kugel (mit Zurücklegen) ziehen, um mit einer Wahrscheinlichkeit von mindestens 80% mindestens 2-mal "weiß" zu ziehen?

Antwort: mindestens ?-mal

Lösung:

Hier handelt es sich um eine Bernoulli-Kette unbekannter Länge n. Die Trefferwahrscheinlichkeit ("weiß") beträgt 1/8. Damit ergibt sich:

X ≥ 2

≥

0,8

Gegenereignis

X ≤ 1

≤

0,2

Erläuterung zu den beiden letzten Zeilen: Das Gegenereignis von "X ≥ 2" (mindestens 2-mal) ist "X ≤ 1" (höchstens 1-mal). Ereignis und Gegenereignis ergänzen sich bzgl. ihrer Wahrscheinlichkeit zu 1. Wenn die Wahrscheinlichkeit des Ereignisses größer oder gleich 0,8 ist, muss logischerweise die Wahrscheinlichkeit des Gegenereignisses kleiner oder gleich 0,2 sein.

≤

0,2

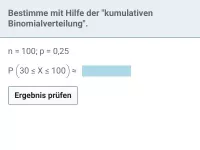
Jetzt musst du die kumulative Binomialverteilung in Abhängigkeit von n tabellieren oder durch Probieren die gesuchte Mindestanzahl ermitteln:

n ≥ 23 denn:

0,1987

20%

und

0,2195

20%

Es muss also mindestens 23-mal eine Kugel mit Zurücklegen gezogen werden.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Lösung mit dem GTR (falls zugelassen):

≤

0,2

binomcdf

n,1/8,0,1

≤

0,2

Zum Tabellieren gehst du folgendermaßen vor:

In Spalte A erzeugst du eine Folge (Englisch: sequence) von natürlichen Zahlen, die für die Länge der Bernoullikette stehen. Der Befehl dazu lautet:

seq

n,n,1,100,1

Es bedeutet, dass nun in Spalte A die natürlichen Zahlen von 1 bis 100 in Schrittweite 1 aufgelistet werden, also: 1, 2, 3, 4, …

In Spalte B erzeugst du eine Folge der gesuchten Wahrscheinlichkeit, die in jeder Zeile zur Länge der Bernoullikette passt. Der Befehl dazu lautet:

seq

binomcdf(n,1/8,0,1),n,1,100,1

Es bedeutet, dass zu jeder Zahl n von 1 bis 100 in Schrittweite 1 jeweils die Wahrscheinlichkeit berechnet wird, also in Zeile 1: binomcdf(1,1/8,0,1), in Zeile 2: binomcdf(2,1/8,0,1), in Zeile 3: binomcdf(3,1/8,0,1), usw.

Wenn du beide Spalten erzeugt hast, suchst du in Spalte B, ab wann die gesuchte Wahrscheinlichkeit kleiner als 20% ist. Hast du die entsprechende Zeile gefunden, so siehst du in Spalte A die passende Länge der Bernoullikette n.

Beispiel 3

Die Verarbeitung von Bauteilen wird als "sehr gut" bezeichnet, wenn man in einer Stichprobe von 100 Stück mit einer Mindestwahrscheinlichkeit von 96% maximal 3 defekte Bauteile findet. Wie hoch darf der Anteil an defekten Bauteilen maximal sein?

Antwort:

? % (gerundet auf eine Dezimale)

Lösung:

Du nimmst an, dass die defekten Bauteile unabhängig von einander auftauchen und somit die Anzahl X der defekten Bauteile binomialverteilt ist. Dann handelt es sich hier um eine Bernoulli-Kette der Länge 100 mit unbekannter Trefferwahrscheinlichkeit ("defektes Bauteil") p. Damit ergibt sich:

X ≤ 3

≥

0,96

100

;

≥

0,96

Durch Probieren oder Ablesen aus einer Tabelle erhält man, dass der Prozentsatz an defekten Bauteilen maximal 1,2 % sein darf, da:

100

;

0,012

96,72%

≥

96%

und

100

;

0,013

95,8%

≤

96%

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Lösung mit dem GTR (falls zugelassen):

100,

≥

0,96

binomcdf

100,p,0,3

≥

0,96

Zum Tabellieren gehst du folgendermaßen vor:

In Spalte A erzeugst du eine Folge (Englisch: sequence) von Dezimalzahlen zwischen 0 und 1, die für die Trefferwahrscheinlichkeit p der Bernoullikette stehen. Es ist sinnvoll, die Trefferwahrscheinlichkeit auf ein Zehntel Prozent genau angeben zu können. Der Befehl dazu lautet:

seq

p,p,0,1,0.001

Es bedeutet, dass nun in Spalte A die Zahlen von 0 bis 1 in Schrittweite 0,001 also 0,1% aufgelistet werden, also: 0, 0.001, 0.002, 0.003, …

In Spalte B erzeugst du eine Folge der gesuchten Wahrscheinlichkeit, die in jeder Zeile zur Trefferwahrscheinlichkeit passt. Der Befehl dazu lautet:

seq

binomcdf(100,p,0,3),p,0,1,0.001

Es bedeutet, dass zu jeder Zahl p von 0 bis 1 in Schrittweite 0,001 jeweils die Wahrscheinlichkeit

X ≤ 3

berechnet wird, also in Zeile 1: binomcdf(100,0,0,3), in Zeile 2: binomcdf(100,0.001,0,3), in Zeile 3: binomcdf(100,0.002,0,3), usw.

Wenn du beide Spalten erzeugt hast, suchst du in Spalte B, ab wann die gesuchte Wahrscheinlichkeit größer als 96% ist. Hast du die entsprechende Zeile gefunden, so siehst du in Spalte A die passende Trefferwahrscheinlichkeit der Bernoullikette.

Beispiel 4

150; p

0,3

X ≥ 50

≈ ▇

Lösung allgemein (unabhängig vom Hilfsmittel)

X ≥ 50

X > 49

−

X ≤ 49

−

150;0,3

Für die markierte Wahrscheinlichkeit liest man (anhand des Hilfsmittels) ab: 0,78987

X ≥ 50

≈

−

0,78987

0,21013

mit GTR (falls zugelassen)

Hier kommt der Befehl binomcdf(n,p,untere Grenze,obere Grenze) zur Anwendung. Wenn man die untere Grenze weglässt, dann wird sie automatisch gleich Null gesetzt.

Hier gilt also:

X ≥ 50

50 ≤ X ≤ 150

binomcdf

150,0.3,50,150

≈

0,21013

oder:

X ≥ 50

−

X ≤ 49

−